Advertisements
Advertisements
प्रश्न
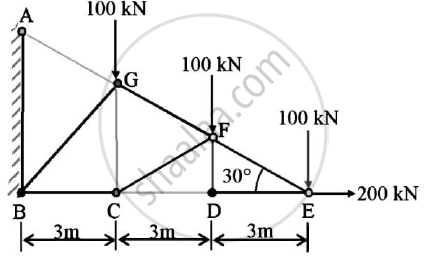
Referring to the truss shown in the figure. Find :
(a) Reaction at D and C
(b)Zero force members.
(c)Forces in member FE and DC by method of section.
(d)Forces in other members by method of joints.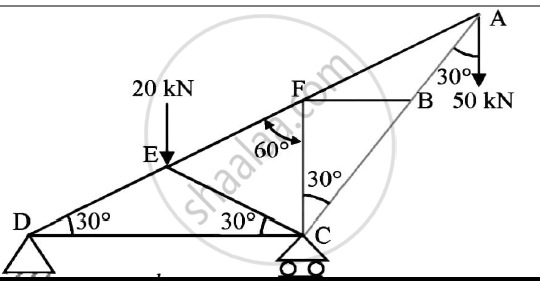
उत्तर
By Geometry:
In Δ ADC, ∠ADC = ∠CAD = 30o
AC = CD = l
Similarly, in Δ EDC,
ED = EC
Δ DEG and Δ CEG are congruent
DG = GC =`1/2`
In Δ DEG, ∠EDG=30o, ∠DGE=90o
tan30= `(EG)/(DG)`
EG = DG.tan30 =`I/2x1/sqrt3=I/(2sqrt3)`
In Δ ACH,
CH =`(AC)/2=I/2`
DH = DC + CH = l +`I/2=(3I)/2`
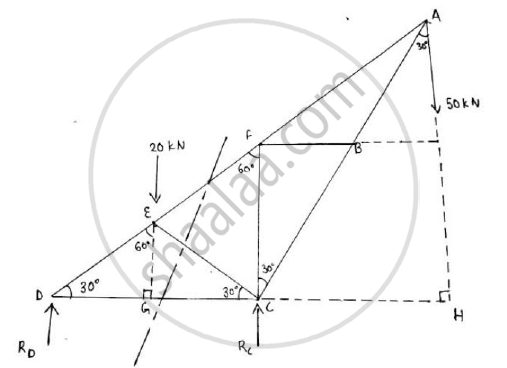
No horizontal force is acting on the truss, so no horizontal reaction will be present at point A The truss is in equilibrium Applying the conditions of equilibrium
Σ MD = 0
-20 x DG -50 x DH + RC x DC = 0
-20 x`1/(2)50X(3I)/2+RCX1=0`
-10 - 75 + RC = 0
RC = 85 kN
Σ Fy=0
-20 – 50 + RD + RC=0
RD = -15kN
Loading at point B and F is shown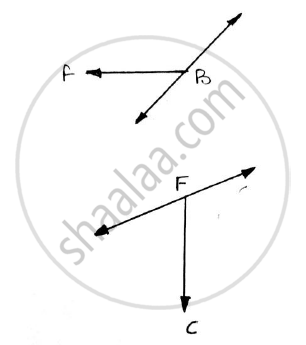
As per the rule,member BF will have zero force and is a zero force number. Similarly,Member CF will have zero force
Method of sections :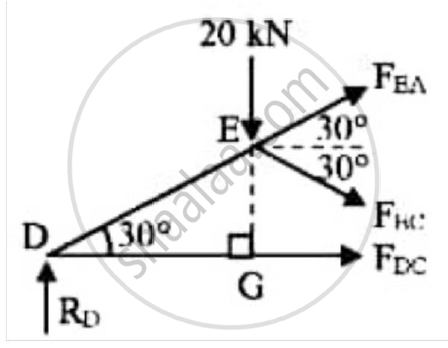
Applying the conditions of equilibrium to the section shown
Σ MD = 0
-20 x DG – FECcos 30 x EG - FECsin30 x DG = 0
-20 x `I/2` x - FECcos30 x EG - FECsin30 x DG = 0
-20 x`I/2`x -FEC x `sqrt3/2x(I/2)-`FEC x`1/2XI/2`=0
-10 x l - FEC x`I/4`-FEC x`I/4`=0
`-(2I)/4F_(EC)=10L`
FEC = -20kN
RD – 20 - FECsin30 + FEAsin30 = 0
-15 - 20 + 20 x 0.5 + FEA x 0.5 = 0
FECcos30 + FEAcos30 + FDC = 0
-20 x 0.866 + 50 x 0.866 + FDC = 0
FDC = - 25.9808kN
Method of joints: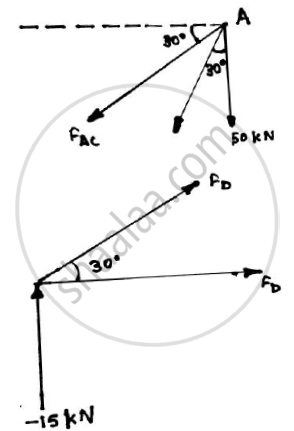
Joint A
-50 - FAEsin30 - FACcos30 = 0
-50 - 50 x 0.5 = FAC x 0.866
FAC = -86.6025kN
Joint D
FDC + FDEcos30 = 0
-25.9808 + 0.866FDE = 0
FDE = 30kN
Final answer :
| Member | Magnitude (in kN) | Nature |
| AE (AF and EF) | 50 | Tension |
| AC (AB and BC) | 86.6025 | Compression |
| EC | 20 | Compression |
| DE | 30 | Tension |
| DC | 25.9808 | Compression |
| FB | 0 | |
| FC | 0 |
APPEARS IN
संबंधित प्रश्न
What is a zero force member in a truss? With examples state the conditions for a zero force member.
In the truss shown in figure,compute the forces in each member.
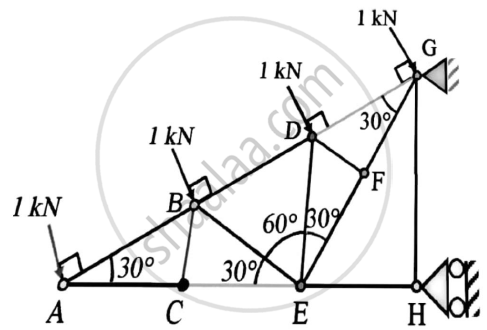
A truss is loaded and supported as shown.Determine the following:
(1)Identify the zero force members,if any
(2)Find the forces in members EF,ED and FC by method of joints.
(3)Find the forces in members GF,GC and BC by method of sections