Advertisements
Advertisements
प्रश्न
Represent to solution set of each of the following inequations graphically in two dimensional plane:
6. x ≤ 8 − 4y
उत्तर
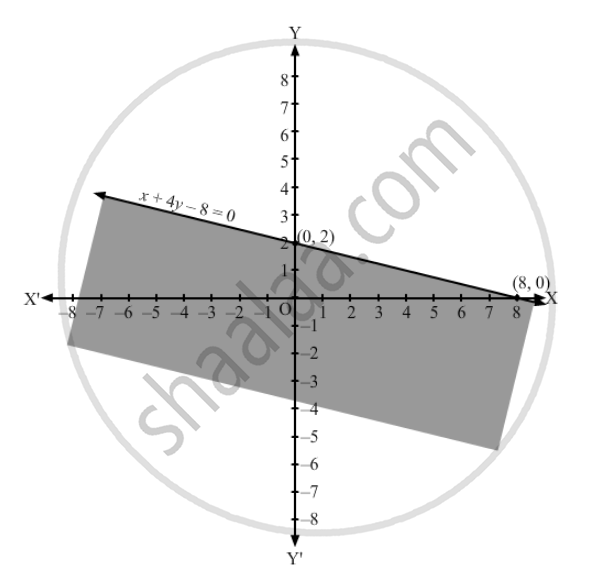
Converting the inequation to equation, we obtain x + 4y \[-\]8 = 0
Putting y = 0 and x = 0 in this equation, we obtain x = 8 and y = 2 respectively. So, this line meets the x-axis at (8,0) and y-axis at (0,2). We plot these points and join them by a thick line. This divides the xy plane into two parts. To determine the region represented by the given inequality, consider point O(0,0). Clearly, (0,0) satisfies the inequality. So, the region containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
APPEARS IN
संबंधित प्रश्न
Solve 24x < 100, when x is a natural number.
Solve 24x < 100, when x is an integer.
Solve –12x > 30, when x is an integer.
Solve 5x – 3 < 7, when x is an integer.
Solve 5x – 3 < 7, when x is a real number.
Solve the given inequality for real x: 4x + 3 < 5x + 7.
Solve the given inequality for real x: 3x – 7 > 5x – 1.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x: x + `x/2` + `x/3` < 11
Solve the given inequality for real x: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
Solve the given inequality and show the graph of the solution on number line:
3x – 2 < 2x +1
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5 cm longer than the second?
[Hint: If x is the length of the shortest board, then x, (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x = (x + 3) + 2x ≤ 91 and 2x ≥ (x + 3) + 5]
Solve the inequality.
2 ≤ 3x – 4 ≤ 5
Solve the inequality.
`-12 < 4 - (3x)/(-5) <= 2`
Solve the inequality.
`7 <= (3x + 11)/2 <= 11`
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2y − y ≤ 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
5. −3x + 2y ≤ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
0 ≤ 2x − 5y + 10
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3y ≥ 6 − 2x
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3x − 2y ≤ x + y − 8
Solutions of the inequalities comprising a system in variable x are represented on number lines as given below, then ______.![]()
State whether the following statement is True or False.
If xy < 0, then x > 0, and y > 0
State whether the following statement is True or False.
If |x| < 5, then x ∈ (–5, 5)
State whether the following statement is True or False.
Graph of x > –2 is
Solution of a linear inequality in variable x is represented on number line given below ______.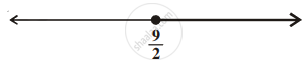
Solution of a linear inequality in variable x is represented on number line given below ______.

If x > –2 and x < 9, then x ∈ (– 2, 9)
If |x| > 5, then x ∈ (– `oo`, – 5) ∪ [5, `oo`)
