Question

Seg AM is a median of ∆ABC. If AB = 22, AC = 34, BC = 24, find AM

Answer 1

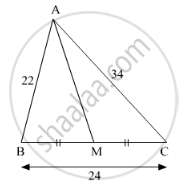
In ∆ABC, point M is the midpoint of side BC.

\[BM = MC = \frac{1}{2}BC = 12\]

\[{AB}^2 + {AC}^2 = 2 {AM}^2 + 2 {BM}^2 \left( \text{by Apollonius theorem} \right)\]
\[ \Rightarrow \left( 22 \right)^2 + \left( 34 \right)^2 = 2 {AM}^2 + 2 \left( 12 \right)^2 \]
\[ \Rightarrow 484 + 1156 = 2 {AM}^2 + 288\]
\[ \Rightarrow 1640 - 288 = 2 {AM}^2 \]
\[ \Rightarrow 1352 = 2 {AM}^2 \]
\[ \Rightarrow {AM}^2 = 676\]
\[ \Rightarrow AM = 26\]

Hence, AM = 26.