Question

Show that all harmonics are present on a stretched string between two rigid supports.

Show that all harmonics are present in case of a stretched string.

Answer 1

Fundamental mode:

Modes of vibrations in stretched string:-

a. Consider a string stretched between two rigid supports and plucked. Due to plucking, string vibrates and loops are formed in the string. Vibrations of string are as shown in figure.

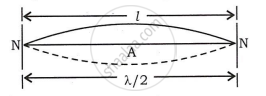
b. Let,

p = number of loops

l = length of string

∴ Length of one loop = l /p         ......(1)                                 

Two successive nodes form a loop. Distance between two successive nodes is λ/2.

∴ Length of one loop = λ/2           .......(2) 

From equations (1) and (2),

λ/2 = l/p

∴ λ = 2l/p                                      ....(3)

Velocity of transverse wave is given by,

`v=sqrt(T/m)`

Frequency of string is given by,

n = v/λ

Substituting λ from equation (3),

`n=sqrt(T/m)/((2l)/p)`

`thereforen=p/(2l)sqrt(T/m)`           ......(4)

Fundamental mode or first harmonic:-

In this case, p = 1

∴ From equation (4),

`n=1/(2l)sqrt(T/m)`

This frequency is called fundamental frequency.

First overtone or second harmonic:-

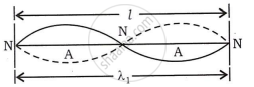
In this case, p = 2

∴ From equation (4),

`n_1=2/(2l)sqrt(T/m)=2xx1/(2l)sqrt(T/m)=2n`

`thereforen_1=2n`

Second overtone or third harmonic:-

In this case, p = 3

Using equation (4),

`n_2=3/(2l)sqrt(T/m)=3xx1/(2l)sqrt(T/m)=3n`

`thereforen_2=3n`

(p - 1)^th overtone or p^th harmonic:-

`n_((p-1))=pxx1/(2l)sqrt(T/m)=pn`

For the overtone,

`n_p=(p+1)/(2l)sqrt(T/m)=(p+1)n`

Thus, in the vibration of stretched string, frequencies of vibrations are n, 2n, 3n,…..so on.

Hence, all harmonics (even as well as odd) are present in the vibrations of stretched string.