Advertisements
Advertisements
प्रश्न
Show that the velocity of a traveling wave produced in a string is v = `sqrt("T"/mu)`.
उत्तर
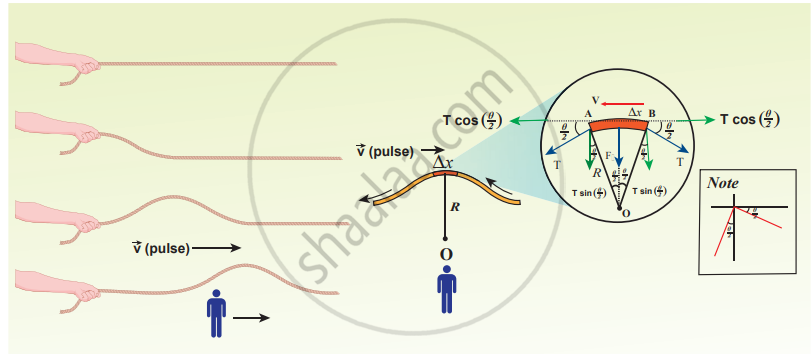
Let us consider an elemental segment in the string as shown in the Figure. Let A and B be two points on the string at an instant of time. Let dl and dm be the length and mass of the elemental string, respectively. By definition, linear mass density, μ is
(a) Transverse waves in a stretched string
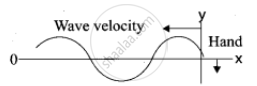
(b) Elemental segment in a stretched string is zoomed and the pulse seen from an observer frame who moves with velocity v.
`mu = ("dm"/"dl")` ...(1)
dm = μ dl … (2)
Consider an elemental string AB having a curvature which looks like an arc of a circle with centre at O, radius R and the arc subtending an angle θ at the origin O as shown in Figure. The angle 0 can be written in terms of arc length and radius as `"dl"/"R"` = θ. The centripetal acceleration supplied by the tension in the string is
`"a"_"cp" = "v"^2/"R"` ....(3)
Then, centripetal force can be obtained when mass of the string (dm) is included in equation (3)
`"F"_"cp" = (("dm")"v"^2)/"R"` ....(4)
Experienced by elemental string can be calculated by substituting equation (2) in equation (4) we get the centripetal force as
`(("dm")"v"^2)/"R" = (mu"v"^2"dl")/"R"` ...(5)
The tension T acts along the tangent of the elemental segment of the string at A and B. Since the arc length is very small, variation in the tension force can be ignored. T can be resolved into horizontal component T cos `(theta/2)` and vertical component T sin `(theta/2)`.
The horizontal components at A and B are equal in magnitude but opposite in direction. Hence, they cancel each other. Since the elemental arc length AB is taken to be very small, the vertical components at A and B appears to acts vertical towards the centre of the arc and hence, they add up. The net radial force Fr is
Fr = 2Tsin`(theta/2)` ...(6)
Since the amplitude of the wave is very small when it is compared with the length of the string, the sine of small angle is approximated
as sin `(theta/2) ≈ theta/2`.
Hence, equation (6) can be written as,
`"F"_"r" = 2"T" xx theta/2 = "T"theta` ...(7)
But `theta = "dl"/"R"`, therefore substituting in equation (7), we get
`"F"_"r" = "T" "dl"/"R"` ...(8)
Applying Newton’s second law to the elemental string in the radial direction, under equilibrium, the radial component of the force is equal to the centripetal force. By equating equation (5) and equation (8), we get,
`"T" "dl"/"R" = mu"v"^2 "dl"`
v = `sqrt("T"/mu)` measured in ms-1
APPEARS IN
संबंधित प्रश्न
A student tunes his guitar by striking a 120 Hertz with a tuning fork, and simultaneously plays the 4th string on his guitar. By keen observation, he hears the amplitude of the combined sound oscillating thrice per second. Which of the following frequencies is the most likely the frequency of the 4th string on his guitar?
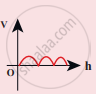
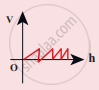
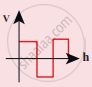
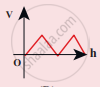
Compare the velocities of the wave forms given below, and choose the correct option.
where, vA, vB, vC and vD are velocities given in (a), (b), (c) and (d), respectively.
The displacement y of a wave travelling in the x direction is given by y = (2 x 10-3) sin `(300 "t" - 2x + pi/4)`, where x and y are measured in metres and t in second. The speed of the wave is:
A uniform rope having mass m hangs vertically from a rigid support. A transverse wave pulse is produced at the lower end. Which of the following plots shows the correct variation of speed v with height h from the lower end?