Advertisements
Advertisements
प्रश्न
Show by using the graphical method that: `s=ut+1/2at^2` where the symbols have their usual meanings.
उत्तर
Suppose the body travels a distance (s) in time (t).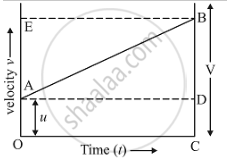
In the figure, the distance travelled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC.
Thus: Distance travelled = Area of the trapezium OABC
But, Area of the figure OABC = Area of rectangle OADC + Area of triangle ABD
= Area of rectangle OADC + area of triangle ABD
Now, find out the area of rectangle OADC and area of triangle ABD.
(i) Area of rectangle OADC
= (OA) (OC)
= (u) (t)
(ii) Area of triangle ABD,
= (1/2)(AD)(BD)
= (1/2)(t)(at)
= (1/2)at2
Distance travelled (s) is,
So, s = Area of rectangle OADC + Area of triangle ABD
`s = ut + 1/2at^2`
This is the second equation of motion.
Where
(s) - Displacement
(u) - Initial velocity
(a) - Acceleration
(t) - Time
APPEARS IN
संबंधित प्रश्न
What is the quantity which is measured by the area occupied below the velocity-time graph?
What can you say about the motion of a body if its speed-time graph is a straight line parallel to the time axis ?
The velocity-time graph for part of a train journey is a horizontal straight line. What does this tell you about its acceleration ?
Draw a velocity-time graph for the free fall of a body under gravity starting from rest. Take g = 10m s-2
Represent the position of a body described as at 15 m, 30o north of west, on a graph paper.
What can you conclude if the speed-time graph of a body is a straight line sloping upwards and not passing through the origin?
Which of the following graphs represents a motion with negative acceleration?
Its time-displacement graph is a straight line.
Figure shows the distance-time graph of three students A, B and C. On the basis of the graph, answer the following :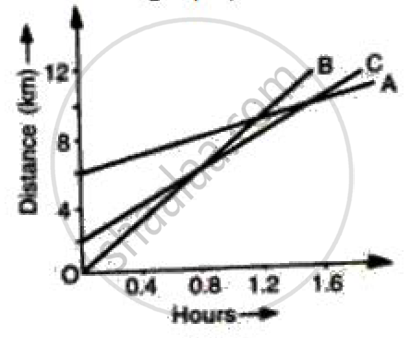
Which of the three is traveling the fastest?
The area under the v-t graph represents a physical quantity that has the unit.
