Advertisements
Advertisements
प्रश्न
समांतरभुज चौकोनाच्या दोन लगतच्या बाजूंचे गुणोत्तर 3 : 4 आहे जर त्याची परिमिती 112 सेमी असेल तर त्याच्या प्रत्येक बाजूची लांबी काढा.
उत्तर
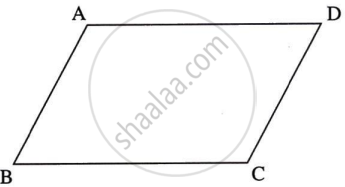
समजा, `square`ABCD हा समांतरभुज चौकोन आहे.
AB : BC = 3 : 4
जर AB = 3x सेमी
म्हणून, BC = 4x सेमी ...(x हा सामाईक गुणक आहे.)
∴ CD = AB = 3x सेमी आणि AD = BC = 4x सेमी ...(समांतरभुज चौकोनाच्या संमुख भुजा)
`square`ABCD ची परिमिती = 112 सेमी
∴ AB + BC + CD + AD = 112
∴ 3x + 4x + 3x + 4x = 112
∴ 14x = 112
∴ x = `112/14`
∴ x = 8
∴ CD = AB = 3x = 3 × 8 = 24 सेमी
∴ AD = BC = 4x = 4 × 8 = 32 सेमी
APPEARS IN
संबंधित प्रश्न
एका समांतरभुज चौकोनाची परिमिती 150 सेमी आहे आणि एक बाजू दुसरीपेक्षा 25 सेमी मोठी आहे. तर त्या समांतरभुज चौकोनाच्या सर्व बाजूंची लांबी काढा.
एका समांतरभुज चौकोनाच्या लगतच्या दोन कोनांचे गुणोत्तर 1 : 2 आहे. तर त्या समांतरभुज चौकोनाच्या सर्व कोनांची मापे काढा.
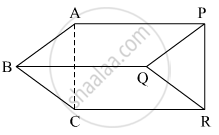
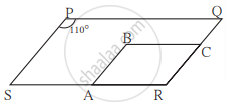
खालील आकृती मध्ये `square`PQRS व `square`ABCR हे दोन समांतरभुज चौकोन आहेत. ∠P = 110° तर `square`ABCR च्या सर्व कोनांची मापे काढा.
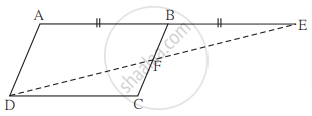
खालील आकृती मध्ये `square`ABCD समांतरभुज चौकोन आहे. किरण AB वर बिंदू E असा आहे की BE = AB. तर सिद्ध करा, की रेषा ED ही रेख BC ला F मध्ये दुभागते.
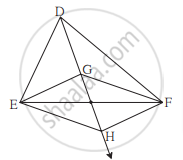
खालील आकृती मध्ये, बिंदू G हा ΔDEF चा मध्यगा संपात आहे. किरण DG वर बिंदू H असा घ्या, की D-G-H आणि DG = GH, तर सिद्ध करा `square`GEHF समांतरभुज आहे.
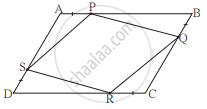
खालील आकृती मध्ये `square`ABCD ह्या समांतरभुज चौकोनाच्या बाजूंवर P, Q, R, S बिंदू असे आहेत की, AP = BQ = CR = DS तर सिद्ध करा, की `square`PQRS हा समांतरभुज चौकोन आहे.
खालील आकृती मध्ये रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तर सिद्ध करा की, रेख BC || रेख QR व रेख BC ≅ रेख QR.