Question

Solve the following problem.

The figure below shows a block of mass 35 kg resting on a table. The table is so rough that it offers a self-adjusting resistive force 10% of the weight of the block for its sliding motion along with the table. A 20 kg wt load is attached to the block and is passed over a pulley to hang freely on the left side. On the right side, there is a 2 kg wt pan attached to the block and hung freely. Weights of 1 kg wt each, can be added to the pan. Minimum how many and maximum how many such weights can be added into the pan so that the block does not slide along the table?

Answer 1

Frictional (resistive) force f = 10% (weight)

`= 10/100 xx 35 xx 10 = 35`N

1. Consider FBD for 20 kg-wt loads. Initially, the block kept on the table is moving towards the left, because of the movement of the block of mass 20 kg in a downward direction
Thus, for a block of mass 20 kg,
ma = mg - T₁     .....(1)

Consider the forces acting on the block of mass 35 kg in a horizontal direction only as shown in figure (b). Thus, the force equation for this block is,

m₁a = T₁ - T₂ - f      .....(2)

To prevent the block from sliding across the table,

m₁a = ma = 0

∴ T₁ = mg = 200N    ......[From (1)]

T₁ = T₂ + f                 ......[From (2)]

∴ T₂ + f = 200

∴ T₂ = 200 - 35 = 165 N

Thus, the total force acting on the block from the right-hand side should be 165 N.

∴ Total mass = 16.5 kg

∴ Minimum weight to be added

= 16.5 - 2 = 14.5 kg

≈ 15 weights of 1 kg each

2. Now, considering motion of the block towards right, the force equations for the masses in the pan and the block of mass 35 kg can be determined from FBD shown

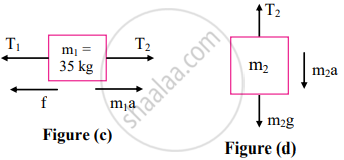
From figure (c)

m₁a = T₂ - T₁ - f       .....(iii)

From figure (d),

m₂a = m₂g - T₂        ....(iv)

To prevent the block of mass 35 kg from sliding across the table,

m₁a = m₂a = 0

∴ From equations (iii) and (iv),

T₂ = T₁ + f

T₂ = m₂g

∴ m₂g = 200 + 35 = 235 N

∴ The maximum mass required to stop the sliding

= 23.5 – 2 = 21.5 kg ≈ 21 weights of 1 kg each