Advertisements
Advertisements
प्रश्न
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
आलेख
बेरीज
उत्तर
To find the graphical solution, construct the table as follows:
| Inequation | Equation | Double intercept form | Points (x1,x2) | Points (x1,x2) |
| 3x + y ≥ 27 | 3x + y = 27 | `x/9+y/27=1` |
A(9,0) B(0,27) |
3(0) + 0 ≥ 27 0 ≥ 27 ∴ Non-origin side |
| x + y ≥ 21 | x + y = 21 | `x/21+y/21=1` |
C(21,0) D(0,21) |
(0) + 0 ≥ 21 ∴ 0 ≥ 21 ∴ Non-origin side |
| x ≥ 0 | x = 0 | - | - | R.H.S of Y-axis |
| y ≥ 0 | y = 0 | - | - | above X-axis |
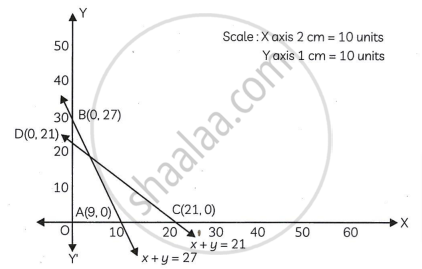
BHC is the unbounded feasible region with B = (0, 27) and C = (21,0)
Point H is the point of intersection of lines
3x + y = 27 ...(i)
x + y = 21 ...(ii)
Subtracting (ii) from (i),
3x + y = 27
x + y = 21
– – –
2x = 6
∴ x = 3
Put x =3 in (ii), 3 + 4 = 21
∴ y = 18
∴ H = (3,18)
Objective function, Z = 4x + 24
| Feasible points | The value of Z = 4x + 2y |
| B (0,27) | Z = 4(0) + 2(27) = 54 |
| H (3,18) | Z = 4(3) + 2(18) = 12 + 36 = 48 |
| C (21,0) | Z = 4(21) + 2(0) = 84 + 0 = 84 |
∴ At H (3,18) the value of Z is minimum.
Hence Z has minimum value 48, when x = 3, y = 18.
shaalaa.com
Linear Programming Problem (L.P.P.)
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
