Advertisements
Advertisements
प्रश्न
State and prove Bernoulli’s theorem for a flow of incompressible, non-viscous, and streamlined flow of fluid.
उत्तर
Bernoulli’s theorem: According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant.
Mathematically,
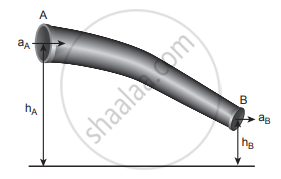
Flow of liquid through a pipe AB
`"P"/"ρ" + 1/2 "v"^2 + "gh"` = constant
This is known as Bernoulli’s equation.
Proof: Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t which is equal to the volume of the liquid leaving B at the same time. Let aA, vA and PA be the area of cross-section of the tube, velocity of the liquid and pressure exerted by the liquid at A respectively.
Let the force exerted by the liquid at A is FA = PAaA
Distance travelled by the liquid in time t is d = vAt
Therefore, the work done is W = FAd = PAaAvAt
But aAvAt = aAd = V, volume of the liquid entering at A.
Thus, the work done is the pressure energy (at A), W = FAd = PAV
Pressure energy per unit volume at A = `"Pressure energy"/"Volume" = ("P"_"A""V")/"V"` = PA
Pressure energy per unit mass at A = `"Pressure energy"/"Mass" = ("P"_"A""V")/"m" = "P"_"A"/("m"/"V") = "P"_"A"/ρ`
since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is
EPA = `"P"_"A""V" = "P"_"A""V" xx ("m"/"m") = "m"("P"_"A")/ρ`
Potential energy of the liquid at A,
PEA = mg hA
Due to the flow of liquid, the kinetic energy of the liquid at A,
KEA = `1/2"m" "v"_"A"^2`
Therefore, the total energy due to the flow of liquid at A,
EA = EPA + KEA + PEA
EA = `"m"("P"_"A")/ρ + 1/2"mv"_"A"^2 + "mg" "h"_"A"`
Similarly, let aB, vB and PB be the area of cross-section of the tube, the velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at EB, we get
EB = `"m"("P"_"B")/ρ + 1/2"mv"_"B"^2 + "mg" "h"_"B"`
From the law of conservation of energy, EA = EB
`"m"("P"_"A")/ρ + 1/2"mv"_"A"^2 + "mg" "h"_"A" = "m"("P"_"B")/ρ + 1/2"mv"_"B"^2 + "mg" "h"_"B"`
`("P"_"A")/ρ + 1/2"v"_"A"^2 + "gh"_"A" = ("P"_"B")/ρ + 1/2"v"_"B"^2 + "gh"_"B"` = constant
Thus, the above equation can be written as
`"P"/(ρ"g") + 1/2 "v"^2/"g" + "h"` = constant
The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But in practice, some energy is lost due to friction. This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal pipe, then
h = 0 ⇒ `"P"/(ρ"g") + 1/2 "v"^2/"g"` = constant
APPEARS IN
संबंधित प्रश्न
State Bernoulli’s theorem.
What are the energies possessed by a liquid? Write down their equations.
What happens to the pressure inside a soap bubble when air is blown into it?
State the principle and usage of the Venturimeter.
Obtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
Describe the construction and working of venturimeter and obtain an equation for the volume of liquid flowing per second through a wider entry of the tube.
The reading of the pressure meter attached with a closed pipe is 5 × 105 Nm−2. On opening the valve of the pipe, the reading of the pressure meter is 4.5 × 105 Nm−2. Calculate the speed of the water flowing in the pipe.
A sniper fires a rifle bullet into a gasoline tank making a hole 53.0 m below the surface of gasoline. The tank was sealed at 3.10 atm. The stored gasoline has a density of 660 kgm−3. The velocity with which gasoline begins to shoot out of the hole is (Take g = 10 m/s2).
