Advertisements
Advertisements
प्रश्न
State whether the two triangles are congruent or not. Justify your answer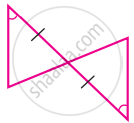
उत्तर
Let the given triangles be ∆ABC and ∆CDE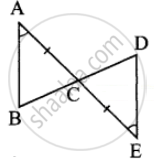
Here `bar("AC") = bar("CE")` ...(given)
∠BAC = ∠DEC ...(given)
∠ACB = ∠DCE ...(vertically opposite angles)
Two angles and the included side are equal.
Therefore by ASA criterion ∆ABC ≅ ∆CDE.
APPEARS IN
संबंधित प्रश्न
In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that ∆BCF ≡ ∆EDF.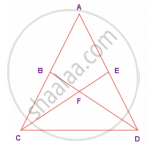
In the figure, ∠TMA ≡∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that ΔPIN ~ ΔATM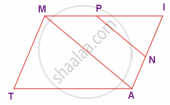
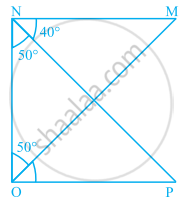
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion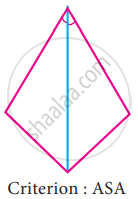
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion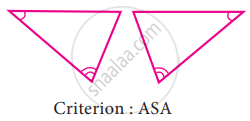
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal
Two triangles are congruent, if two angles and the side included between them in one of the triangles are equal to the two angles and the side included between them of the other triangle. This is known as the ______.
In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.
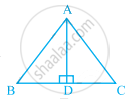
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
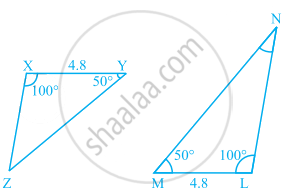
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
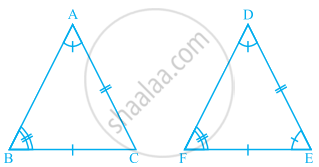
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.