Question

Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.

Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.

पर्याय

• Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

• Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).

• Assertion (A) is true but reason(R) is false.

• Assertion (A) is false but reason(R) is true.

Answer 1

Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

Explanation:

Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.

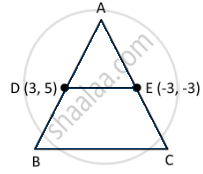
We need to use the theorem in Reasoning

The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.

DE = `1/2` BC

2DE = BC

BC = 2DE

BC = `2 xx sqrt((-3 - 3)^2 + (-3 - 5)^2)`

BC = `2 xx sqrt((-6)^2 + (-8)^2)`

BC = `2 xx sqrt(6^2 + 8^2)`

BC = `2 xx sqrt(36 + 64)`

BC = `2 xx sqrt(100)`

BC = 2 × 10

BC = 20 cm

Thus, Assertion is true.

Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.

This is always true.

Here is a proof

In ΔABC,

D is the mid-point of AB

⇒ AD = DB

⇒ `(AD)/(DB)` = 1  ......(1)

E is the mid-point of AC

⇒ AE = EC

⇒ `(AE)/(EC)` = 1  ......(2)

From (1) and (2)

`(AD)/(DB) = (AE)/(EC)`  .....(If a line divides any two sides of a triangles in the same ratio, 3 then the line is parallel to the third side)

∴ DE || BC

Hence proved

Thus, Reasoning is true.