Advertisements
Advertisements
प्रश्न
The 16th term of an AP is 5 times its 3rd term. If its 10th term is 41, find the sum of its first 15 terms.
उत्तर
Let a be the first term and d be the common difference of the AP. Then,
a16 = 5 × a3 (Given)
⇒ a+ 15d = 5 (a +2d) [ an = a + (n-1) d]
⇒ a + 15 d = 5a + 10d
⇒ 4a = 5d
Also,
a10 = 41 (Given)
⇒ a +9d -41 ..............(2)
Solving (1) and (2), we get
`a + 9 xx (4a)/5 = 41 `
`⇒ (5a +36a)/5 =41`
`⇒ (41a)/5 = 41`
⇒ a = 5
Putting a = 5 in (1), we get
5d = 4 × 5 =20
⇒ d = 4
`"Using the formula " s_n = n/2 [2a + (n-1) d] , `we get
`S_15 = 15/2 [2 xx 5 + (15 -1) xx 4]`
`=15/2 xx (10 +56)`
`= 15/2 xx 66`
=495
Hence, the required sum is 495.
APPEARS IN
संबंधित प्रश्न
An AP 8, 10, 12, … has 60 terms. Find its last term. Hence, find the sum of its last 10 terms.
A man arranges to pay off debt of ₹36000 by 40 monthly instalments which form an arithmetic series. When 30 of the installments are paid, he dies leaving on-third of the debt
unpaid. Find the value of the first instalment.
Which of the following sequences are A.P.? If they are A.P. find the common difference.
–10, –6, –2, 2,...
Which of the following sequences are A.P. ? If they are A.P. find the common difference .
127, 132, 137,...
Write the correct number in the given boxes from the following A. P.
1, 8, 15, 22,...
Here a =Here a = t1 =
t1 =  , t2 =
, t2 =  , t3 =
, t3 =  ,
,
t2 – t1 =  –
–  =
= 
t3 – t2 =  –
–  =
=  ∴ d =
∴ d = 
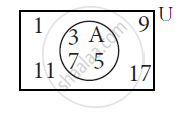
Observe the adjacent Venn diagram and write the complement of A.
Write a trinomial of degree 7.
Yogesh requires 3 days more than Vivek to do a work completely. If both
of them work together, the work can be completed in 2 days. Find the
number of days required for each of them to do the work completely.
Find out the ratio of 1 mm to 1 cm.
If for an A.P. the first term is 2 and the common difference is 3, then find first three-term of A.P.
