Advertisements
Advertisements
प्रश्न
The acceleration of the moon just before it strikes the earth in the previous question is
पर्याय
10 m s−2
0⋅0027 m s−2
6⋅4 m s−2
5⋅0 m s−2
Advertisements
उत्तर
6⋅4 m s−2
According to the previous question, we have :
Radius of the moon, \[R_m = \frac{R_e}{4} = \frac{6400000}{4} = 1600000 m\]
So, when the Moon is just about to hit the surface of the Earth, its centre of mass is at a distance of (Re + Rm) from the centre of the Earth.
Acceleration of the Moon just before hitting the surface of the earth is given by
\[g' = \frac{GM}{( R_e + R_m )^2} = \frac{GM}{{R_e}^2 (1 + \frac{R_m}{R_e} )^2}\]
\[ \Rightarrow g' = \frac{g}{(1 + \frac{R_m}{R_e} )^2} = \frac{10}{(1 + \frac{1}{4} )^2} = \frac{10 \times 16}{25}\]
\[ \Rightarrow g' = 6 . 4 m/ s^2\]
APPEARS IN
संबंधित प्रश्न
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed 250 N on the surface?
An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?
The acceleration of moon with respect to earth is 0⋅0027 m s−2 and the acceleration of an apple falling on earth' surface is about 10 m s−2. Assume that the radius of the moon is one fourth of the earth's radius. If the moon is stopped for an instant and then released, it will fall towards the earth. The initial acceleration of the moon towards the earth will be
Take the effect of bulging of earth and its rotation in account. Consider the following statements :
(A) There are points outside the earth where the value of g is equal to its value at the equator.
(B) There are points outside the earth where the value of g is equal to its value at the poles.
What is the acceleration due to gravity on the top of Mount Everest? Mount Everest is the highest mountain peak of the world at the height of 8848 m. The value at sea level is 9.80 m s−2.
A body is weighed by a spring balance to be 1.000 kg at the North Pole. How much will it weigh at the equator? Account for the earth's rotation only.
A particle is fired vertically upward from earth's surface and it goes up to a maximum height of 6400 km. Find the initial speed of particle.
A mass of 6 × 1024 kg (equal to the mass of the earth) is to be compressed in a sphere in such a way that the escape velocity from its surface is 3 × 108 m s−1. What should be the radius of the sphere?
If the acceleration due to gravity becomes 4 times its original value, then escape speed ____________.
Explain the variation of g with altitude.
Explain the variation of g with depth from the Earth’s surface.
One can easily weigh the earth by calculating the mass of the earth by using the formula:
The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity ______.
Which of the following options are correct?
- Acceleration due to gravity decreases with increasing altitude.
- Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density).
- Acceleration due to gravity increases with increasing latitude.
- Acceleration due to gravity is independent of the mass of the earth.
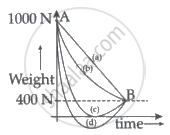
A person whose mass is 100 kg travels from Earth to Mars in a spaceship. Neglect all other objects in the sky and take acceleration due to gravity on the surface of the Earth and Mars as 10 m/s2 and 4 m/s2 respectively. Identify from the below figures, the curve that fits best for the weight of the passenger as a function of time.
If R is the radius of the earth and g is the acceleration due to gravity on the earth's surface, the mean density of the earth is ______.
A ball is immersed in water kept in container and released. At the same time container is accelerated in horizontal direction with acceleration, `sqrt44` m/s2. Acceleration of ball w.r.t. container is ______ m/s2 (specific gravity of ball = 12/17, g = 10 m/s2)
If the radius of the earth shrinks by 2% while its mass remains the same. The acceleration due to gravity on the earth's surface will approximately ______.
