Question

The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.

पर्याय

• `10 (sqrt3 + 1)`

• `5 sqrt3`

• `5 (sqrt3 + 1)`

• `10 sqrt3`

Answer 1

The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower `underline(10 (sqrt3 + 1))`.

Explanation:

Since after moving towards the tower the angle of elevation of the top increases by 15°.

Therefore angle becomes 30° + 15° = 45°

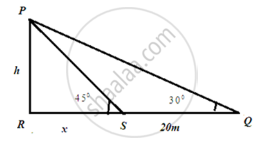
`"tan"  45^circ = "h"/"x"`

`=> 1 = "h"/"x"`

`=> "x" = "h"`

Also,

`"tan"  30^circ = "h"/(20 + "x")`

`=> 1/sqrt3 = "h"/(20 + "h")`

`=> 20 + "h" = "h" sqrt3`

`=> "h" = 20/(sqrt3 - 1)`

`=> "h" = 20/(sqrt3 - 1) xx (sqrt3 + 1)/(sqrt3 + 1)`

`=> "h" = 10 (sqrt3 + 1) "m"`