Question

The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.

पर्याय

• `(10(sqrt(3) - 1), 25)`

• `(10(sqrt(3) - 1), 25/2)`

• `(10(sqrt(3) + 1), 25)`

• `(10(sqrt(3) + 1), 25/2)`

Answer 1

The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is `underlinebb((10(sqrt(3) - 1)","  25))`.

Explanation:

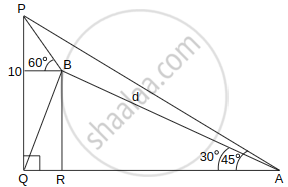
Given lengths are QA = 10

RA = dcos30° = `(sqrt(3)d)/2`

QR = `10 - (sqrt(3)d)/2`

BR = dsin30° = `d/2`

tan60° = `(PQ - BR)/(QR) = (10 - d/2)/(10 - (sqrt(3)d)/2)`

`\implies sqrt(3) = (20 - d)/(20 - sqrt(3)d)`

`\implies 20sqrt(3) - 3d` = 20 – d

`\implies` 2d = `20(sqrt(3) - 1)`

`\implies` d = `10(sqrt(3) - 1)`

ar (PQRB) = α = `1/2(PQ + BR).QR`

= `1/2(10 + d/2).(10 - (sqrt(3)d)/2)`

= `1/2(10 + 5sqrt(3) - 5)(10 - 15 + 5sqrt(3))`

= `1/2(5sqrt(3) + 5)(5sqrt(3) - 5)`

= `1/2(75 - 25)`

= 25