Advertisements
Advertisements
प्रश्न
The dimensions of a solid metallic cuboid are 72 cm × 30 cm × 75 cm. It is melted and recast into identical solid metal cubes with each edge 6 cm. Find the number of cubes formed.
Also, find the cost of polishing the surfaces of all the cubes formed at the rate Rs. 150 per sq. m.
उत्तर
The dimensions of a solid are: 72 cm, 30 cm, 75 cm
The volume of the cuboid = 72 cm x 30 cm x 75 cm = 162000 cm3
Side of a cube = 6 cm
Volume of a cube = 63 = 216 cm3
The number of a cube = ` (162000)/(216) = 750`
The surface area of a cube = 6a2 = 6 x 62 = 216 cm2
Total surface area of 750 cubes = 750 x 216 = 162000 cm2
Total surface area in square metres = `(162000)/(10000)`
= 16.2 square meters
Rates of polishing the surface per square meter = Rs. 150
The total cost of polishing the surface = 150 x 16.2 = Rs. 2430
APPEARS IN
संबंधित प्रश्न
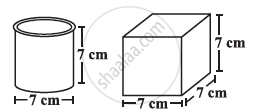
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Fill in the blank in the following so as to make the statement true:
1 m3 = .........cm3
Fill in the blank in the following so as to make the statement true:
1 ml = ........ cu. cm
Find the surface area of a cube whose volume is 216 dm3.
Four identical cubes are joined end to end to form a cuboid. If the total surface area of the resulting cuboid as 648 m2; find the length of the edge of each cube. Also, find the ratio between the surface area of the resulting cuboid and the surface area of a cube.
The volume of a cube is 729 cm3. Find its total surface area.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
The length, breadth, and height of a cuboid are in the ratio 6: 5 : 3. If its total surface area is 504 cm2, find its volume.
Three cubes of sides x cm, 8cm and 10cm respectively are melted and formed into a single cube of edge 12cm, Find 'x'.
A river 2 m deep and 45 m wide is flowing at the rate of 3 km per hour. Find the amount of water in cubic metres that runs into the sea per minute.
