Advertisements
Advertisements
प्रश्न
The displacement of a particle is given by x = (t – 2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is ______.
पर्याय
4 m
8 m
12 m
16 m
उत्तर
The displacement of a particle is given by x = (t – 2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is 8 m.
Explanation:
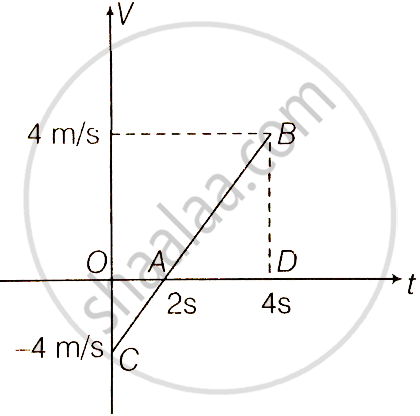
Given, `x = (t - 2)^2`
Velocity, `v = (dx)/(dt) = d/(dt) (t - 2)^2 = 2(t - 2)` m/s
Acceleration, `a = (dv)/(dt) = d/(dt) [2(t - 2)]`
= `2[1 - 0]`
= 2 m/s2
When t = 0; v = – 4 m/s
t = 2s; v = 0 m/s
t = 4s; v = 4 m/s
v-t graph is shown in the adjacent diagram
Distance travelled = Area of the graph
= Area OAC + Area ABD
= `(4 xx 2)/2 + 1/2 xx 2 xx 4`
= 8 m
APPEARS IN
संबंधित प्रश्न
A woman starts from her home at 9.00 am, walks with a speed of 5 km h–1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h–1. Choose suitable scales and plot the x-t graph of her motion.
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with zero speed may have non-zero velocity.
In Exercise, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Suggest a suitable physical situation for the following graph:
In the following figure shows the graph of the x-coordinate of a particle going along the X-axis as a function of time. Find instantaneous velocity at 2, 5, 9 and 12s.

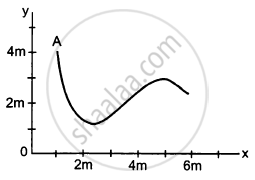
Figure A particle starts from a point A and travels along the solid curve shown in the following figure. Find approximately the position B of the particle such that the average velocity between the position A and B has the same direction as the instantaneous velocity at B.
Write the SI units of speed and average speed.
Two cars are moving with speeds of 40 km/hr due North and 40 km/hr due South respectively. Do they have the same velocity?
In one dimensional motion, instantaneous speed v satisfies 0 ≤ v < v0.
A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 – t); 0 < t < 3 and v(t) = – (t – 3)(6 – t) for 3 < t < 6 s in m/s. It repeats this cycle till it reaches the height of 20 m.
- At what time is its velocity maximum?
- At what time is its average velocity maximum?
- At what time is its acceleration maximum in magnitude?
- How many cycles (counting fractions) are required to reach the top?
