Advertisements
Advertisements
प्रश्न
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee
उत्तर
Given f(x) = 1.23x
Where x represents the number of American dollars
g(y) = 50.50y
where y represents the number of Singapore dollars.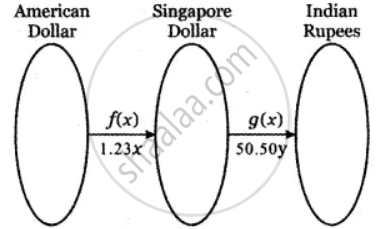
To convert American dollars to Indian rupees
We must find gof(x) = g(f(x))
= g(1.23x)
= 50.50(1.23x)
= 62.115x
∴ The function for the exchange rate of American can dollars in terms of Indian rupees is
gof(x) = 62.115x
APPEARS IN
संबंधित प्रश्न
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer
Write the values of f at − 4, 1, −2, 7, 0 if
f(x) = `{{:(- x + 4, "if" - ∞ < x ≤ - 3),(x + 4, "if" - 3 < x < -2),(x^2 - x, "if" - 2 ≤ x < 1),(x - x^2, "if" 1 ≤ x < 7),(0, "otherwise"):}`
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X → X)
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
not one-to-one but onto
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
one-to-one but not onto
Find the largest possible domain of the real valued function f(x) = `sqrt(4 - x^2)/sqrt(x^2 - 9)`
Find the range of the function `1/(2 cos x - 1)`
Show that the relation xy = −2 is a function for a suitable domain. Find the domain and the range of the function
The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 − x. Express his day revenue, total cost and profit on this meal as functions of x
Choose the correct alternative:
If f(x) = |x − 2| + |x + 2|, x ∈ R, then
Choose the correct alternative:
The range of the function f(x) = |[x] − x|, x ∈ R is
Choose the correct alternative:
The number of constant functions from a set containing m elements to a set containing n elements is
Choose the correct alternative:
If the function f : [−3, 3] → S defined by f(x) = x2 is onto, then S is
Choose the correct alternative:
Let X = {1, 2, 3, 4}, Y = {a, b, c, d} and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is
Choose the correct alternative:
The inverse of f(x) = `{{:(x, "if" x < 1),(x^2, "if" 1 ≤ x ≤ 4),(8sqrt(x), "if" x > 4):}` is
Choose the correct alternative:
The function f : R → R is defined by f(x) = sin x + cos x is
