Advertisements
Advertisements
प्रश्न
The length of a rectangular park is 5 metres more than twice its breadth. If the area of the park is 250 sq. m, find the length and breadth of the park.
उत्तर
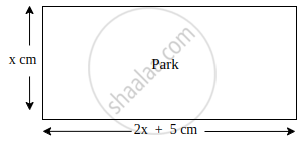
Let the breadth of the rectangular park be x cm.
Then, according to question
Length of the rectangular park be 2x + 5 cm.
Also, given area of rectangular park = 250 cm2
∴ 250 = x(2x + 5)
⇒ 2x2 + 5x – 250 = 0
⇒ 2x2 + 25x – 20x – 250= 0
⇒ x(2x + 25) – 10(2x + 25) = 0
⇒ (2x + 25)(x – 10) = 0
⇒ 2x + 25 = 0 and x – 10 = 0
⇒ x = `-25/2` and x = 10
∴ Breadth, x = 10 cm ...(∵ x can't be negative)
Now, Length = 2(10) + 5 = 25 cm
Hence, the length of the park is 25 cm and breadth of the park is 10 cm.
संबंधित प्रश्न
Check whether the following is the quadratic equation:
(x – 3)(2x + 1) = x(x + 5)
Find the values of a, b, c for the quadratic equation 2x2 = x + 3 by comparing with standard form ax2 + bx + c = 0.
Rs. 7500 were divided equally among a certain number of children. Had there been 20 less children, each would have received Rs. 100 more. Find the original number of children.
Check whether the following is quadratic equation or not.
`x+1/x=x^2`, x ≠ 0
Check whether the following is quadratic equation or not.
x(x + 1) + 8 = (x + 2) (x - 2)
Solve the following equation using the formula:
x2 + 2x – 6 = 0
Solve the following equation by reducing it to quadratic equation:
`sqrt(3x^2 - 2) + 1 = 2x`.
Solve the following equation by using formula :
10ax2 – 6x + 15ax – 9 = 0,a≠0
Solve for x using the quadratic formula. Write your answer correct to two significant figures:
(x – 1)2 – 3x + 4 = 0
The value (values) of x satisfying the equation x2 – 6x – 16 = 0 is ______.
