Advertisements
Advertisements
प्रश्न
The number of lines of symmetry in a 45° – 45° – 90° set-square is ______.
पर्याय
0
1
2
3
उत्तर
The number of lines of symmetry in a 45° – 45° – 90° set-square is 1.
Explanation:
Since, a 45° – 45° – 90° set square has a shape of isosceles triangle and an isosceles triangle has one line of symmetry.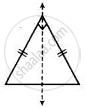
Note: In the given set square two angles are same, it means two sides will be same. So, the shape of set square is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Complete the following figure, about the given lines of symmetry which are shown by dotted lines and name the figure thus obtained:

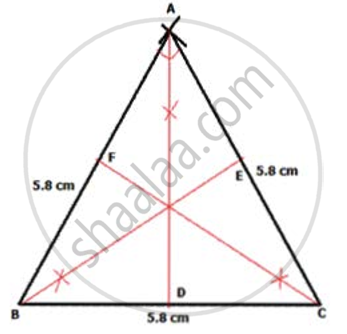
Construct a triangle ABC in which each side measures 5.8 cm. Draw all the possible lines of symmetry.
Draw a diagram and name the figure in the following:
A quadrilateral having only one line of symmetry.
Draw and answer the following.
A triangle which has three lines of symmetry
Which of the following letters does not have the vertical line of symmetry?
Which of the following letters have both horizontal and vertical lines of symmetry?
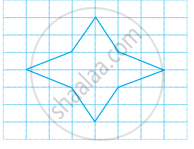
Is there any line of symmetry in the figure? If yes, draw all the lines of symmetry.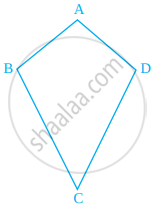
Can you draw a triangle which has exactly two lines of symmetry?
Trace the figure and draw the lines of symmetry, if any:

Trace the figure and draw the lines of symmetry, if any: