Question

Three identical rods each of mass 'M' and length 'L' are joined to form a symbol 'H'. The moment of inertia of the system about one of the sides of 'H' is ______.

पर्याय

• `(2"ML"^2)/3`

• `("ML"^2)/2`

• `("ML"^2)/6`

• `(4"ML"^2)/3`

Answer 1

Three identical rods each of mass 'M' and length 'L' are joined to form a symbol 'H'. The moment of inertia of the system about one of the sides of 'H' is `underline((4"ML"^2)/3)`.

Explanation:

The given situation can be shown as

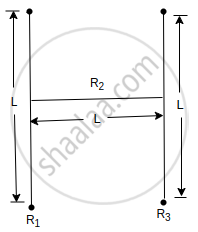
Let us lake the moment of Inertia of the system about rod R₁ then total moment of inertia is

l_T = l₁ + l₂ + l₃    ....(i)

For rod R₁, l₁ = 0

For rod R₂, using perpendicular axis theorem,

`"l"_2 = "ML"^2/3`

For rod R₃, using parallel axis theorem,

`"l"_3 = "l"_"CM" + "l"_("at" "L") = 0 + "ML"^2 = "ML"^2`

Now, putting the values of l₁, l₂ and l₃ in Eq. (i), we get

`"l"_"T" = 0 + "ML"^2/3 + "ML"^2`

`=> "l"_"T" = (4 "ML"^2)/3`