Question

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.

पर्याय

• `sqrt(a^2 + b^2)`

• `sqrt(a^2 - b^2)`

• `2sqrt(a^2 - b^2)`

• `2sqrt(a^2 + b^2)`

Answer 1

`underline(2sqrt(a^2 - b^2))`

Explanation:

Let O be the common center of the two circles and AB be the chord of the larger circle which touches the smaller circle at C.

Join OA and OC.

Then OC ⊥ AB

Let OA = a and OC = b.

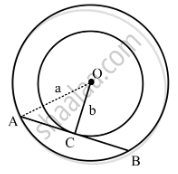
Since OC ⊥ AB, OC bisects AB

[∵ perpendicular from the centre to a chord bisects the chord].

In right Δ ACO, we have

OA² = OC² + AC² [by Pythagoras’ theorem]

⇒ AC = `sqrt("OA"^2 - "OC"^2) =  sqrt(a^2 - b^2)`

∴ AB = 2AC = `2sqrt(a^2 - b^2)` [∵ C is the midpoint of AB]

i.e. Length of the chord AB = `2sqrt(a^2 - b^2)`