Question

Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP

Answer 1

Drop OM and ON perpendicular on AB and CD.
Join OP, OB and OD.

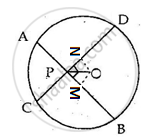
∴ OM and ON bisect AB and CD respectively
(Perpendicular drawn from the centre of a circle to chord bisects it)

∴ MP = `1/2` AB = `1/2` CD = ND       ...........(i)

In rt Δ OMB, OM²= OB² = MB² ………………..(ii)

In rt Δ OND,  ON² = OD² - ND²        ………………..(iii)

From (i),(ii) and (iii)

OM = ON
In ΔOPM and ΔOPN,
∠OMP = ∠ONP    (both 90°)
OP = OP        (Common)
OM = ON        (Proved above)

By Right Angle – Hypotenuse – Side criterion of congruence,

∴ ΔOPM ≅ ΔOPN (by RHS)

The corresponding parts of the congruent triangles are congruent.
∴ PM = PN (c.p.c.t)
Adding (i) to both sides,
MB + PM = ND + PN
⟹ BP = DP
Now, AB = CD
∴ AB – BP = CD – DP (∵ BP = DP)
⟹ AP = CP