Advertisements
Advertisements
प्रश्न
Two opposite angles of a parallelogram are (2x + 60)° and (4x)°. Find the value of x.
उत्तर
Opposite angles of a parallelogram are (2x + 60)° and (4x).
We already know that the opposite angles of a parallelogram are equal.
∴ 2x + 60° = 4x
⇒ 4x – 2x = 60°
⇒ 2x = 60°
⇒ x = 30°
Hence, the value of x is 30°.
APPEARS IN
संबंधित प्रश्न
Show that ABCD is a parallelogram if A = (4, 8), B = (5, 5), C = (2, 4), D = (1, 7)
If P(-2,4), Q(4,8), R(10, 5) and S(4, 1) are the vertices of a quadrilateral, show that it is a parallelogram.
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?
`square`ABCD is cyclic. If ∠B = 110°, then find measure of ∠D.
In figure, points G, D, E, F are concyclic points of a circle with centre C.
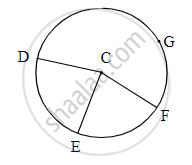
∠ECF = 70°, m(arc DGF) = 200°
Find m(arc DEF) by completing activity.
m(arc EF) = ∠ECF ......[Definition of measure of arc]
∴ m(arc EF) = `square`
But; m(arc DE) + m(arc EF) + m(arc DGF) = `square` .....[Measure of a complete circle]
∴ m(arc DE) = `square`
∴ m(arc DEF) = m(arc DE) + m(arc EF)
∴ m(arc DEF) = `square`
