Question

Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is ______.

पर्याय

• `2pisqrt(d^3/(3"GM"))`

• `1/(2pi) sqrt((3"Gm")/d^3)`

• `1/(2pi) sqrt(d^3/(3"Gm"))`

• `2pisqrt((3"GM")/d^3)`

Answer 1

Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is `bb(2pisqrt(d^3/(3"GM")))`.

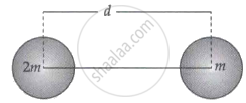
`"X"_"com" = (2"m"xx0+"m"."d")/(2"m"+"m") = "d"/3`

Now, applying force balance equation

F_c = F_g

⇒ `((2"m")"v"^2)/"X"_"com" = ("G"(2"m")."m")/"d"^2`

⇒ `(2"m"(omega"d"/3)^2)/("d"/3) = (2"Gm"^2)/"d"^2`

⇒ `omega^2 = ((2"Gm"^2)/"d"^2)/(2"m""d"/3)`

⇒ `omega = sqrt((2"Gm"^2)/("d"^2 .2)xx3/"md")`

⇒ `omega = sqrt((3"Gm")/"d"^3)`

⇒ `(2pi)/"T" = sqrt((3"GM")/"d"^3)`

⇒ T = `2pisqrt(d^3/(3"Gm"))`