Question

Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`

Answer 1

Let AB be the leaning tower and let C and D be two given stations at distances a and b respectively from the foot A of the tower.

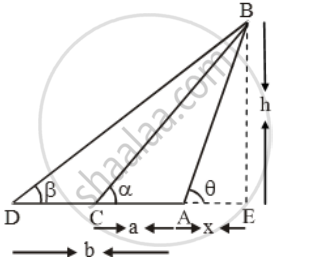
Let AE = x and BE = h

In ∆ABE, we have

`\tan \theta =\frac{BE}{AE}\Rightarrow \tan \theta =\frac{h}{x}`

⇒ x = h cot θ ….(i)

In ∆CBE, we have

`\tan \alpha =\frac{BE}{CE}`

`\Rightarrow \tan \alpha =\frac{h}{a+x}`

⇒ a + x = h cot α

⇒ x = h cot α – a ….(ii)

In ∆DBE, we have

`\tan \beta =\frac{BE}{DE}`

`\Rightarrow \tan \beta =\frac{h}{b+x}`

⇒ b + x = h cot β

⇒ x = h cot β– b ….(iii)

From equations (i) and (ii), we have

h cot θ= h cot α– a

⇒ h (cot α– cot θ) = a

`\Rightarrow h=\frac{a}{\cot \alpha -\cot \theta }`

From equation (i) and (iii), we get

h cot θ= h cot β– b

⇒ h (cot β– cot θ) = b

`\Rightarrow h=\frac{b}{\cot \beta -\cot \theta }`

Equating the values of h from equations (iv) and (v), we get

`\frac{a}{\cot \alpha -\cot \theta }=\frac{b}{\cot \beta -\cot \theta }`

⇒ a(cot β– cot θ) = b(cot α– cot θ)

⇒ (b – a) cot θ= b cot α– a cot β

`\cot \theta =\frac{b\cot \alpha -a\cot \beta }{b-a}`