Advertisements
Advertisements
प्रश्न
Two sticks each of length 7 cm are crossing each other such that they bisect each other at right angles. What shape is formed by joining their end points? Give reason.
उत्तर
Sticks can be treated as the diagonals of a quadrilateral.
Now, since the diagonals (sticks) are bisecting each other at right angles, therefore the shape formed by joining their endpoints will be a rhombus.
APPEARS IN
संबंधित प्रश्न
Diagonals of a parallelogram `square`WXYZ intersect each other at point O. If ∠XYZ = 135° then what is the measure of ∠XWZ and ∠YZW?
If l(OY)= 5 cm then l(WY)= ?
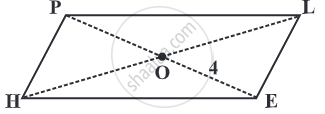
Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.
Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Figure). Show that AC and PQ bisect each other.
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
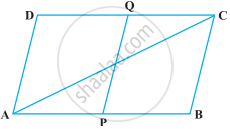
P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
If the diagonals of a quadrilateral bisect each other, it is a ______.
The point of intersection of diagonals of a quadrilateral divides one diagonal in the ratio 1:2. Can it be a parallelogram? Why or why not?
Two sticks each of length 5 cm are crossing each other such that they bisect each other. What shape is formed by joining their endpoints? Give reason.
