Question

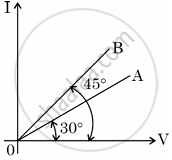
Two wires A and B of different metals have their lengths in ratio 1 : 2 and their radii in ratio 2 : 1 respectively. I-V graphs for them is shown in the figure. Find the ratio of their

1. Resistances (R_A/R_B) and
2. Resistivities (σ_A/σ_B)

Answer 1

Ratio of length = 1 : 2

and radii = 2 : 1

i. Resistance `(R_A/R_B)`

According to Ohm's law, V = IR

`I/V = 1/R`

`(tan(theta_A))/(tan(theta_B)) = R_B/R_A`

⇒ `(tan30^circ)/(tan45^circ) = (R_B)/(R_A)   ...[theta_A = 30^circ, theta_B = 45^circ ("from figure given in question")]`

`R_B/R_A = 1/sqrt3`

∴ The ratio of Resistances (R_A/R_B) is `sqrt3 : 1`.

ii. Here, `A_A/A_B = R_A^2/R_B^2 = 4/1`

and `L_A/L_B = 1/2`

`sigma_A = (R_A A_A)/L_A`

and `sigma_B = (R_B A_B)/L_B`

`sigma_A/sigma_B = R_A/R_B * A_A/A_B * L_B/L_A`

= `sqrt3 * 4/1 * 2/1`

`sigma_A/sigma_B = 8sqrt3`

∴ The ratio of Resistivities (σ_A/σ_B) is `8sqrt3 : 1`.