Question

Using Gauss’s law, show that the electric field `vecE` at a point due to a uniformly charged infinite plane sheet is given by `vecE = sigma/(2epsilon_0)hatn` where symbols have their usual meanings.

Answer 1

Consider a thin, infinite flat sheet of charge with a uniform surface charge density σ. We want to determine the electric field at a point P at a distance of r from it.
The electric field (E) is symmetric and points outwards, normal to the sheet. It must have the same magnitude and opposite direction at two places, P and P', which are equidistant from the sheet and on opposing sides. We select a cylindrical Gaussian surface with cross-sectional area A and length 2r, perpendicular to the sheet.

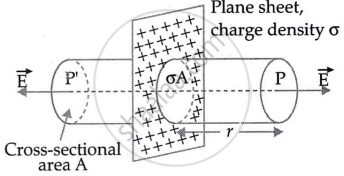
Here, the flux through the curved surface is zero. The flux through the plane-end faces of the cylinder is

Φ_E = EA + EA = 2EA

Charge enclosed by the Gaussian surface, q = σA

According to Gauss's theorem,

`phi_E = q/epsilon_0`

`therefore 2EA = (sigmaA)/epsilon_0`

`E = sigma/(2epsilon_0)`

`vecE = sigma/(2epsilon_0)hatn`

where `hat n` is the unit vector normal to the plane and away from it.