Advertisements
Advertisements
प्रश्न
With the help of a circuit diagram derive the formula for the resultant resistance of three resistances connected:
- in series and
- in parallel
उत्तर
- Resistors in Series:
A series circuit connects the components one after the other to form a ‘single-loop. A series circuit has only one loop through which current can pass. If the circuit is interrupted at any point in the loop, no current can pass through the circuit, and hence no electric appliances connected in the circuit will work. Series circuits are commonly used in devices such as flashlights. Thus, if
- Resistors are connected end to end so that the same current passes through each of them, then they are said to be connected in series.
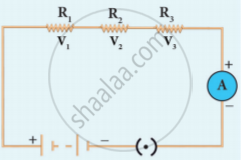
-
Let, three resistances R1, R2, and R3 be connected in series.
-
Let the current flowing through them be I.
-
According to Ohm’s Law, the potential differences V1, V2, and V3 across R1, R2, and R3 respectively, are given by:
V1 = IR1 …. (1)
V2 = IR2 …. (2)
V3 = IR3 …. (3)
The sum of the potential differences across the ends of each resistor is given by:
V = V1 + V2 + V3
using equations (1), (2), and (3), we get
V = IR1 + IR2 + IR3 …. (4) -
The effective resistor is a single resistor, which can replace the resistors effectively, so as to allow the same current through the electric circuit.
-
Let, the effective resistance of the series-combination of the resistors, be RS. Then,
V = IRS ….(5)
Combining equations (4) and (5)
IRS = IR1 + IR2 + IR3
RS = R1 + R2 + R3
Thus, we can understand that -
When a number of resistors are connected in series, their equivalent resistance or effective resistance is equal to the sum of the individual resistances.
-
When V resistors of equal resistance R are connected in series, the equivalent resistance is ‘nR’. i.e., RS = nR
-
The equivalent resistance in a series combination is greater than the highest of the individual resistances.
- Resistors in Parallel:
A parallel circuit has two or more loops through which current can pass. If the circuit is disconnected in one of the loops, the current can still pass through the other loop(s). The wiring in a house consists of parallel circuits.
-
Consider that three resistors R1, R2, and R3 are connected across two common points A and B.
-
The potential difference across each resistance is the same and equal to the potential difference between A and B. This is measured using the voltmeter.
-
The current I arriving at A divides into three branches I1, I2, and I3 passing through R1, R2, and R3 respectively.
According to Ohm’s law, we have,
`"I"_1 = "V"/"R"_1` ....(1)
`"I"_2 = "V"/"R"_2` ....(2)
`"I"_3 = "V"/"R"_3` ....(3)
The total current through the circuit is given by
I = I1 + I2 + I3
Using equations (1), (2) and (3), we get
I = `"V"/"R"_1 + "V"/"R"_2 + "V"/"R"_3` ...(4)
Let the effective resistance of the parallel combination of resistors be RP Then,
I = `"V"/"R"_"P"` ...(5)
Combining equations (4) and (5), we have
`"V"/"R"_"P" = "V"/"R"_1 + "V"/"R"_2 + "V"/"R"_3`
`1/"R"_"P" = 1/"R"_1 + 1/"R"_2 + 1/"R"_3` -
When a number of resistors are connected in parallel, the sum of the reciprocals of the individual resistances is equal to the reciprocal of the effective or equivalent resistance.
-
When ‘n’ resistors of equal resistances R are connected in parallel, the equivalent resistance is `"R"/"n"`
`1/"R"_"P" = 1/"R" + 1/"R" + 1/"R" ... + 1/"R" = "n"/"R"`
Hence, `"R"_"P" = "R"/"n"`
-
The equivalent resistance in a parallel combination is less than the lowest of the individual resistances.
APPEARS IN
संबंधित प्रश्न
Judge the equivalent resistance when the following are connected in parallel − (a) 1 Ω and 106Ω, (b) 1 Ω and 103Ω and 106Ω.
A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio `"R"/"R'"` is ______.
Name the material which is the best conductor of electricity.
In series combination of resistances ______.
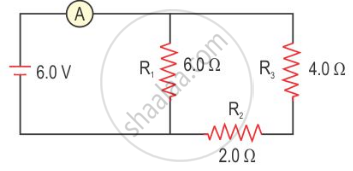
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of emf 6.0 V as shown in the following figure. Calculate :
- the effective resistance of the circuit.
- the reading of ammeter.
How does the resistance of an alloy, vary with temperature?
What material is used for making wire to prepare heating coils? Give a reason.
State a relation between electrical power, resistance and potential difference in an electrical circuit.
Illustrate-combination of cells e.g., three cells, in parallel, explaining the combination briefly. Obtain an expression for current ‘i’ in the combination.
Two resistors having 2Ω and 3Ω resistance are connected—(i) in series, and (ii) in parallel. Find the equivalent resistance in each case.
