Advertisements
Advertisements
प्रश्न
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
उत्तर
Let p : Two triangles are not congruent
q : Areas of two triangles are not equal.
∴ Symbolic form of the given statementt is P → q.
Converse : q → p
i.e. If areas of two triangles are not equal then U are not cong:ruent.
Inverse : ~p → ~q
i.e. If two triangles are congruent then their a reas are equal.
Contrapositive : ~q → ~ p
i.e. If areas of two triangles are equal then they congruent.
APPEARS IN
संबंधित प्रश्न
Evaluate: ∫ x . log x dx
Write the following compound statement symbolically.
Hima Das wins gold medal if and only if she runs fast.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
[(p → q) ∧ q] → p
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following statement pattern.
∼ p ∧ [(p ∨ ∼ q) ∧ q]
Construct the truth table of the following:
[(∼p ∨ q) ∧ (q → r)] → (p → r)
Express the following statement in symbolic form.
Milk is white or grass is green.
Write the truth value of the following statement.
The Himalayas are the highest mountains but they are part of India in the North East.
Write the negation of the following statement.
2 + 3 ≠ 5
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Find the truth value of the following statement.
3 is a prime number and an odd number.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is not holiday or Ram studies on holiday.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
Fill in the blanks :
Conjunction of two statement p and q is symbolically written as ______.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
3 is prime number if 3 is perfect square number.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
x3 + y3 = (x + y)3 if xy = 0.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∧ ∼ r
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Write the negation of the following statement.
10 > 5 and 3 < 8
Write the negation of the following statement.
I will have tea or coffee.
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
Write the negation of the following statement.
∃ x ∈ A, such that x + 5 < 11.
If p → q is an implication, then the implication ∼ q → ∼ p is called its
Find the negation of 10 + 20 = 30
Write the following compound statements symbolically.
Triangle is equilateral or isosceles
Write the following statements in symbolic form
Even though it is not cloudy, it is still raining
If (p ∧ ~ r) → (~ p ∨ q) is a false statement, then respective truth values of p, q and r are ______.
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
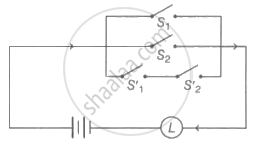
If q: There are clouds in the sky then p: it is raining. The symbolic form is ______
The negation of (p ∨ ∼q) ∧ q is ______
Which of the following is NOT true for p → q.
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
Express the following compound statement symbolically:
3 + 8 ≥ 12 if and only if 5 × 4 ≤ 25
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
