Advertisements
Advertisements
Question
0.5 kg द्रव्यमान का एक कण ν = `"a x"^(3/2)` वेग से सरल रेखीय मति करता है, जहाँ a = `"5 m"^(-1/2)` s-1 है। x = 0 से x= 2m तक इसके विस्थापन में कुल बल द्वारा किया गया कार्य कितना होगा?
Solution
कण का द्रव्यमान m = 0.5 kg
ν = `"a x"^(3/2)` ...(जहाँ a = `5 "मी"^(-1/2)` से-1)
x = 0 पर वेग ν0 = `5 "मी"^(-1/2)` से-1 × 0 = 0
x = 2 मी पर वेग ν = `5 "मी"^(-1/2)` से-1 × `2 "मी"^(3/2)`
= `10sqrt2` मी/से
कार्य - ऊर्जा प्रमेय के अनुसार,
बल द्वारा किया गया कार्य, W = कण की गतिज ऊर्जा में वृद्धि
= `1/2 "m""ν"^2 - 1/2 "m""ν"_0^2`
= `1/2 "m"("ν"^2 - "ν"_0^2)`
= `1/2 "m""ν"^2` (∵ ν0 = 0)
W = `1/2 xx 0.5 "kg" xx (10sqrt2 "मी"//"से"^2) `
= 50 जूल
APPEARS IN
RELATED QUESTIONS
चित्र में कुछ एकविमीय स्थितिज ऊर्जा-फलनों के उदाहरण दिए गए हैं। कण की कुल ऊर्जा कोटि-अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बंताइए, यदि कोई हैं तो जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों।
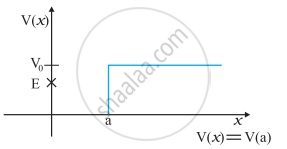

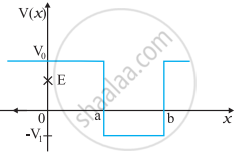
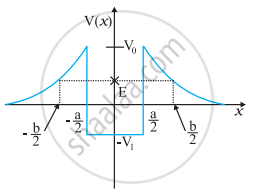
रेखीय सरल आवर्त गति कर रहे किसी कण का (d) स्थितिज ऊर्जा फलन v (x) = 1/2 kx2/2 है, जहाँ k दोलक का बल नियतांक है। k = 0.5 N m-1 के लिए v (x) व x के मध्य ग्राफ चित्र में दिखाया गया है। यह दिखाइए कि इस विभव के अंतर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही ‘वापस आना चाहिए जब यह x = ± 2 m पर पहुँचता है।
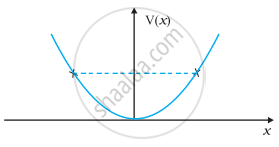
जब कोई संरक्षी बल किसी वस्तु पर धनात्मक कार्य करता है तो वस्तु की स्थितिज ऊर्जा ______।
