Question

`int 1/(x^2 + 1)^2 dx` = ______.

Options

• `tan^-1 x - 1/(2x(x^2 + 1)) + c`

• `1/2tan^-1 x + x/(2(x^2 + 1)) + c`

• `tan^-1 x + x/(x^2 + 1) + c`

• `tan^-1 x + 1/(2(x^2 + 1)) + c`

Answer 1

`int 1/(x^2 + 1)^2 dx` = `underlinebb(1/2tan^-1 x + x/(2(x^2 + 1)) + c)`.

Explanation:

Let I = `int 1/(x^2 + 1)^2 dx`

Put x = tan θ

`\implies` dx = sec²θ dθ.

`\implies I = int (sec^2θ  dθ)/(tan^2θ + 1)^2 = int (sec^2θ)/(sec^4θ) dθ`

`\implies I = intcos^2θ  dθ = 1/2 int (cos2θ + 1)dθ`

`\implies I = 1/4 sin 2θ + θ/2 + c`  ...(1)

∵ tan θ = x

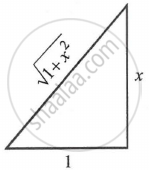
`\implies` sin θ = `x/sqrt(1 + x^2)` and cos θ = `1/sqrt(1 + x^2)`.

`\implies` sin 2θ = 2 sin θ cos θ = `(2x)/((1 + x^2))`. 

∴ I = `1/2. x/((1 + x^2)) + 1/2 tan^-1 x + c`.