Advertisements
Advertisements
Question
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear?
Solution
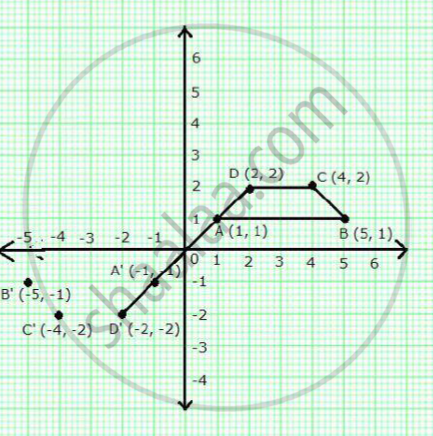
Quadrilateral ABCD is an isosceles trapezium.
Co-ordinates of A’, B’, C’ and D’ are A'(–1, –1), B'(–5, –1), C'(–4, –2) and D'(–2, –2) respectively.
It is clear from the graph that D, A, A’ and D’ are collinear.
APPEARS IN
RELATED QUESTIONS
- Point P (a, b) is reflected in the x-axis to P’ (5, –2). Write down the values of a and b.
- P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
- Name a single transformation that maps P’ to P”.
The point (–2, 0) on reflection in a line is mapped to (2, 0) and the point (5, –6) on reflection in the same line is mapped to (–5, –6).
- State the name of the mirror line and write its equation.
- State the co-ordinates of the image of (–8, –5) in the mirror line.
A point P (–2, 3) is reflected in line x = 2 to point P’. Find the co-ordinates of P’.
A point P (a, b) is reflected in the x-axis to P’ (2, –3). Write down the values of a and b. P” is the image of P, reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line, parallel to y-axis, such that x = 4.
P and Q have co-ordinates (0, 5) and (–2, 4).
- P is invariant when reflected in an axis. Name the axis.
- Find the image of Q on reflection in the axis found in (a).
- (0, k) on reflection in the origin is invariant. Write the value of k.
- Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.
The triangle ABC, where A is (2, 6), B is (–3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C".
- Write down the co-ordinates of A", B" and C".
- Write down a single transformation that maps triangle ABC onto triangle A"B"C".
- The point P (2, –4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
- The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
- Name the figure PQR.
- Find the area of figure PQR.
A’ and B’ are images of A (-3, 5) and B (-5, 3) respectively on reflection in y-axis. Find: (
a) the co-ordinates of A’ and B’.
(b) Assign special name of quadrilateral AA’B’B.
(c) Are AB’ and BA’ equal in length?
Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
Use a graph paper for this question.
(Take 2 cm = 1 unit on both x and y axes)
- Plot the following points: A(0, 4), B(2, 3), C(1, 1) and D(2, 0).
- Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B', C', D' respectively.
- Join the points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation to the line about which if this closed figure obtained is folded, the two parts of the figure exactly coincide.
