Question

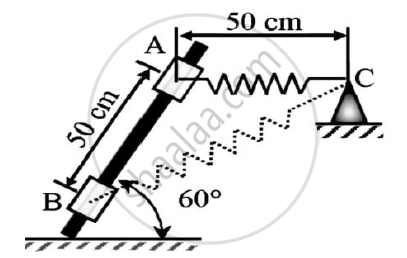
A 50 N collar slides without friction along a smooth and which is kept inclined at 60o to the horizontal.
The spring attached to the collar and the support C.The spring is unstretched when the roller is at A(AC is horizontal).
Determine the value of spring constant k given that the collar has a velocity of 2.5 m/s when it has moved 0.5 m along the rod as shown in the figure.

Answer 1

Given : W=50 N
AB = AC = 0.5 m
To find : Spring constant
Solution :
Mass of collar = `50/g` kg
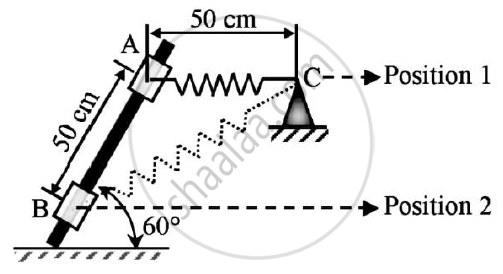
Let us assume that h = 0 at position 2
POSITION 1 :
x = 0
E_s1 = `1/2` x k x x₁² = 0
h₁ = 0.5sin60 = 0.433 m
PE1=mgh1=21.65 J
vA = 0 m/s
KE₁ = 0J
POSITION II :
v_B = 2.5 m/s
PE₂ = mgh = 0 J (because h=0)
KE₂ = `1/2` 𝑋 𝑚 𝑣² = 12 𝑋 `50/g` 𝑋 2.5²
= 15.9276 J
In △ABC
Applying cosine rule
BC² = AB² + AC² -2 X AB X AC X cos(BAC)
= 0.5² + 0.5² – 2 x 0.5 x 0.5 x cos120
= 0.75
BC = 0.866 m
Un-stretched length of the spring = 0.5 m
Extension of spring(x) = 0.866 - 0.5
=0.366 m
E_s2 = `1/2` x k x₂²
= 0.067k
APPLYING WORK ENERGY PRINCIPLE
U_1-2 = KE₂ - KE₁
PE₁ - PE₂ + ES₁ - ES₂ = KE₂ - KE₁

21.6506-0+0-0.067K=15.9276-0

K = 85.4343 N/m
SPRING CONSTANT IS 85.4343 N/m