Advertisements
Advertisements
Question
A ball is bouncing elastically with a speed 1 m/s between walls of a railway compartment of size 10 m in a direction perpendicular to walls. The train is moving at a constant velocity of 10 m/s parallel to the direction of motion of the ball. As seen from the ground ______.
- the direction of motion of the ball changes every 10 seconds.
- speed of ball changes every 10 seconds.
- average speed of ball over any 20 second interval is fixed.
- the acceleration of ball is the same as from the train.
Solution
b, c and d
Explanation:
In this problem, we have to observe the motion from different frames. Here the problem can be solved by the frame of the observer but here we must be clear that we are considering the motion from the ground so we just keep in mind the motion from the frame of observer. Compared to the velocity of trains (10 m/s) speed of the ball is less (1 m/s).
The speed of the ball before collision with the side of train is 10 + 1 = 11 m/s Speed after collision with side of the train = 10 – 1 = 9 m/s As speed is changing after travelling 10 m and speed is 1 m/s, hence time duration of the changing speed is 10 s.
Since the collision of the ball is perfectly elastic there is no dissipation of energy, hence total momentum and kinetic energy are conserved.
Since the train is moving with a constant velocity, hence it will act as an inertial frame of reference as that of Earth and acceleration will be the same in both frames.
Remember: We should not confuse non-inertial and inertial frame of reference. A frame of reference that is not accelerating will be inertial.
APPEARS IN
RELATED QUESTIONS
At a metro station, a girl walks up a stationary escalator in time t1. If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be ______.
For the one-dimensional motion, described by x = t – sint
- x (t) > 0 for all t > 0.
- v (t) > 0 for all t > 0.
- a (t) > 0 for all t > 0.
- v (t) lies between 0 and 2.
A spring with one end attached to a mass and the other to a rigid support is stretched and released.
- Magnitude of acceleration, when just released is maximum.
- Magnitude of acceleration, when at equilibrium position, is maximum.
- Speed is maximum when mass is at equilibrium position.
- Magnitude of displacement is always maximum whenever speed is minimum.
Give examples of a one-dimensional motion where
- the particle moving along positive x-direction comes to rest periodically and moves forward.
- the particle moving along positive x-direction comes to rest periodically and moves backward.
A motor car moving at a speed of 72 km/h can not come to a stop in less than 3.0 s while for a truck this time interval is 5.0 s. On a highway the car is behind the truck both moving at 72 km/h. The truck gives a signal that it is going to stop at emergency. At what distance the car should be from the truck so that it does not bump into (collide with) the truck. Human response time is 0.5 s.
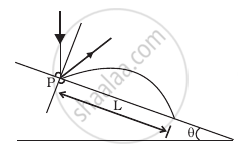
A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle θ with speed vo and rebounds elastically (Figure). Find the distance along the plane where if will hit second time.
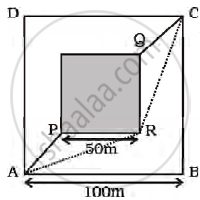
A man wants to reach from A to the opposite corner of the square C (Figure). The sides of the square are 100 m. A central square of 50 m × 50 m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square, he can walk only at a speed of v m/s (v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
A ball is travelling with uniform translatory motion. This means that ______.
Why are porcelain objects wrapped in paper or straw before packing for transportation?
The displacement vector of a particle of mass m is given by `r(t) = hati` A cos ωt + `hatj` B sin ωt. Show that the trajectory is an ellipse.
The displacement vector of a particle of mass m is given by r(t) = `hati` A cos ωt + `hatj` B sin ωt. Show that F = − mω2r.
