Question

A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level

Answer 1

Let C be the centre of the balloon and O be the position of the observer at the horizontal line OX.

Let OA and OB be the tangents to the balloon so that ∠AOB = α, ∠XOC = β and

CA = CB = γ.

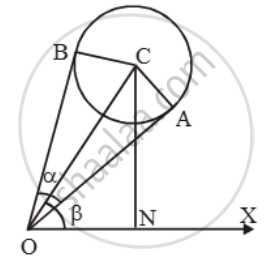
Clearly, right angled triangles OAC and OBC are congruent.

∠AOC = ∠BOC = α/2.

Let CN ⊥ OX.

`\text{Now, }\frac{OC}{CA}=\text{cosec }\frac{\alpha }{2} `

`\Rightarrow OC=\gamma \text{ cosec }\frac{\alpha}{2}\text{ }...\text{(i)}`

`\text{Also, }\frac{CN}{OC}=\sin \beta `

`\Rightarrow CN=OC\text{ sin }\beta =\gamma \text{ cosec }\frac{\alpha }{2}\sin \beta \`