Question

A beam of light is travelling from region II to region III (see the figure). The refractive index in the region I, II and III are n₀​, `​"n"_0/sqrt2`​​ and `"n"_0/sqrt2`​​ respectively. The angle of incidence θ for which the beam just misses entering region III is ______.

Region I	Region II	Region III
n0	n0`sqrt2`	n0`sqrt2`

Options

• 30°

• 45°

• 60°

• sin^-1`(sqrt2)`

Answer 1

A beam of light is travelling from region II to region III (see the figure). The refractive index in the region I, II and III are n₀​, `​"n"_0/sqrt2`​​ and `"n"_0/sqrt2`​​ respectively. The angle of incidence θ for which the beam just misses entering region III is 30°.

Explanation:

The critical angle for region II and III

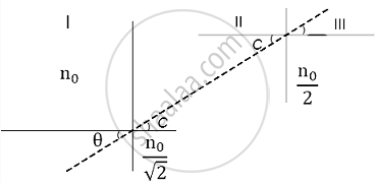
sin C = `mu_"III"/mu_"II"=("n"_0/2)/("n"_0/sqrt2)=1/sqrt2`

ie. ∠C = 45°

The ray, if incident at 45° at the interface of II and III it will be totally internally reflected.

Now, from Snell's lay in region I and II.

n₀ sinθ = `"n"_0/sqrt2` sinC

Or sinθ = `1/sqrt2xxsin`45°

Or sinθ = `1/sqrt2xx1/sqrt2`

Or sinθ = `1/2`

Or sinθ = 30°