Question

A bob of a simple pendulum has mass m and is oscillating with an amplitude a. If the length of the pendulum is L, then the maximum tension in the string is [cos 0° = 1, g = acceleration due to gravity]

Options

• mg`[1 + ("a"/"L")^2]`

• mg`[1 - ("L"/"a")^2]`

• mg`[1 + ("L"/"a")^2]`

• mg`[1 - ("a"/"L")^2]`

Answer 1

mg`[1 + ("a"/"L")^2]`

Explanation:

Consider the figure shown below

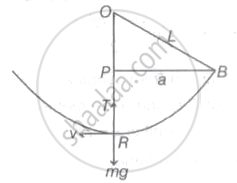
The string posses maximum tension when bob Is at the mean position of oscillation i.e., at position R.

From geometry, OP = `sqrt("L"^2 - "a"^2)`

Also, RP = OR - OP = L - `sqrt("L"^2 - "a"^2)`

The whole kinetic energy of bob at position R is converted into its potential energy at position B.

`therefore 1/2 "mv"^2 = "mg" ("L" - sqrt("L"^2 - "a"^2))`

`"v"^2 = "2g" ("L" - sqrt("L"^2 - "a"^2))`

Balancing forces at R,

T - mg = `"mv"^2/l = (2"mg" ("L" - sqrt("L"^2 - "a"^2)))/"L"`

∴ T = mg + 2mg `(1 - sqrt(1 - "a"^2/"L"^2))`

Using approximation, `sqrt(1 - x^2) = 1 - x^2/2`for x << 1, we get

T = mg + 2mg `[1 - (1 - "a"^2/"2L"^2)]`

= mg + mg`("a"/"L")^2`

`= "mg"[1 + ("a"/"L")^2]`

OR

tension in the string is maximum when the bob passes through the mean position.

`T_{max} = mg + (mV^2)/L`  .........................(1)

In S.H.M. velocity at the mean position is given by V = aω

For simple pendulum T = `2pi sqrt(L/g)`

∴ `omega = (2pi)/T = sqrt(g/L)`

∴ V = `a sqrt(g/L)` or `V^2 = a^2 g/L`

Putting this value of V² in Eq. (1) we get

`T_"max" = mg[1 + (a/L)^2]`