Question

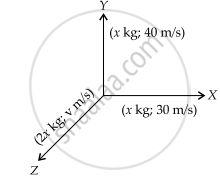
A body of mass M at rest explodes into three pieces, in the ratio of masses 1:1:2. Two smaller pieces fly off perpendicular to each other with velocities of 30 ms^-1 and 40 ms^-1 respectively. The velocity of the third piece will be:

Options

• 15 ms^-1

• 25 ms^-1

• 35 ms^-1

• 50 ms^-1

Answer 1

25 ms^-1

Explanation:

In the given problem a body of mass M explodes into three pieces of mass ratio 1:1:2

Thus, the mass of fragments will be x, x, 2x

Hence, M = x + x + 2x = 4x kg

No exterior forces are involved in the explosion process; instead, internal forces are what cause the explosion to happen. Thus, momentum of the system will be conserved.

Initially M is at rest

Pinitial = Pfinal

By law of conservation of momentum x

`"M" × 0 = "M"/4 × 30 hat"i"  + "M"/4 × 40 hat"j" + (2M)/4  vec"v"`

Where `vecv` is the velocity of the third fragment.

`"M"/2vec"v" = -"M"/4 (30hat"i" + 40hat"j")`

`vec"v" = –15 hat"i"  –  20 hat"j"`

Thus, magnitude of `vec"v" = |vec"v"| = sqrt("v"_x^2 + "v"_y^2)`

= `sqrt((-15)^2 + (-20)^2)`

` |vec"v"|  = sqrt625`

= 25 m/s.