Advertisements
Advertisements
Question
A car is travelling along the road at 8 ms-1. It accelerates at 1 ms-2 for a distance of 18 m. How fast is it then travelling ?
Solution
We have to find the final velocity of the moving object. And we have the following information
Initial velocity, (u) = 8 m/s
Acceleration, (a) = 1 m/s2
Distance, (s) = 18 m
So applying 3rd equation of motion to calculate the final velocity,
`ν = sqrt(u^2 + 2as)`
Where,
(a) - Acceleration
(ν) - Final velocity
(u) - Initial velocity
(s) - Distance
Put the values in the above equation to get the value of final velocity,
`ν = sqrt(64 + 36)` m/s
= `sqrt(100)` m/s
= 10 m/s
APPEARS IN
RELATED QUESTIONS
Which of the two can be zero under certain conditions : average speed of a moving body or average velocity of a moving body ?
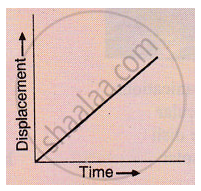
What conclusion can you draw about the velocity of a body from the displacement-time graph shown below :
A boy is sitting on a merry-go-round which is moving with a constant speed of 10 m s−1. This means that the boy is :
Differentiate between uniform acceleration and variable acceleration.
The velocity-time graph of a body in motion is a straight line inclined to the time axis. The correct statement is ___________
When is the negative acceleration?
How can you find the following?
Acceleration from velocity – time graph.
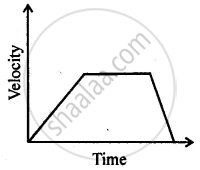
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
A stone thrown vertically upwards takes 3 s to attain maximum height. Calculate
- initial velocity of the stone
- maximum height attained by the stone. (Take g = 9.8 ms−2)
Area under a v – t graph represents a physical quantity which has the unit
