Advertisements
Advertisements
Question
A cell of emf E and internal resistance r is connected to two external resistance R1 and R2 and a perfect ammeter. The current in the circuit is measured in four different situations:
(i) without any external resistance in the circuit
(ii) with resistance R1 only
(iii) with R1 and R2 in series combination
(iv) with R1 and R2 in parallel combination
The currents measured in the four cases are 0.42 A, 1.05 A, 1.4 A and 4.2 A, but not necessarily in the order. Identify the currents corresponding to the four cases mentioned above.
Solution
The current relating to corresponding situations are as follows:
(i) Without any external resistance in the circuit −
`I_1 = E/r`
The current in this case would be maximum, so I1 = 4.2A
(ii) With resistance R1 only −
`I_2 = E/(r + R_1)`
The current in this case will be the second smallest value, so I2 = 1.05 A
(iii) With R1 and R2 in series combination −
`I_3 = E/(r+ (R_1+R_2))`
The current in this case will be minimum as the resistance will be maximum, so I = 0.42 A.
(iv) With R1 and R2 in parallel combination-
`I_4 = E/(r +((R_1R_2)/(R_1 +R_1)))`
The current in this case would be the second largest value, so I = 1.4 A.
APPEARS IN
RELATED QUESTIONS
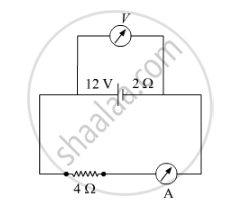
A battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.
(a) Show that a voltmeter when placed across the cell and across the resistor, in turn, gives the same reading.
(b) To record the voltage and the current in the circuit, why is voltmeter placed in parallel and ammeter in series in the circuit?
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance?
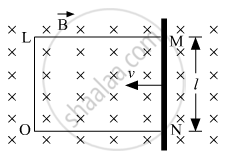
A rectangular conductor LMNO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10 ms−1, calculate the emf induced in the arm. Given the resistance of the arm to be 5 Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm.
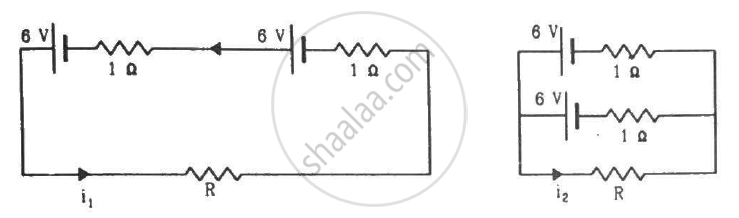
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
Consider N = n1n2 identical cells, each of emf ε and internal resistance r. Suppose n1 cells are joined in series to form a line and n2 such lines are connected in parallel.
The combination drives a current in an external resistance R. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.
A battery of emf 100 V and a resistor of resistance 10 kΩ are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100 Ω, the current through it is constant up to two significant digits.
Find its value. This is the basic principle of a constant-current source.
A coil of resistance 100 Ω is connected across a battery of emf 6.0 V. Assume that the heat developed in the coil is used to raise its temperature. If the heat capacity of the coil is 4.0 J K−1, how long will it take to raise the temperature of the coil by 15°C?
Answer the following question.
A cell of emf E and internal resistance r is connected across a variable resistor R. Plot the shape of graphs showing a variation of terminal voltage V with (i) R and (ii) circuit current I.
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R, versus R.
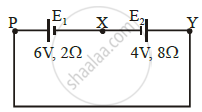
A cell E1 of emf 6 V and internal resistance 2 Ω is connected with another cell E2 of emf 4 V and internal resistance 8 Ω (as shown in the figure). The potential difference across points X and Y is ______.