Question

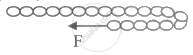
A chain of mass 'M' and length 'L' is put on a rough horizontal surface and is pulled by constant horizontal force 'F' as shown in the figure. The velocity of the chain as it turns completely ______.

(Coefficient of friction = μ)

 

Options

• `{2(F/M - mug)L}^{1/2}`

• `{((2F)/M - mug)L/2}^{1/2}`

• `{2((2F)/M - mug)L}^{1/2}`

• `{((4F)/M - mug)L/2}^{1/2}`

Answer 1

A chain of mass 'M' and length 'L' is put on a rough horizontal surface and is pulled by constant horizontal force 'F' as shown in the figure. The velocity of the chain as it turns completely `underlinebb({2((2F)/M - mug)L}^{1/2})`.

Explanation:

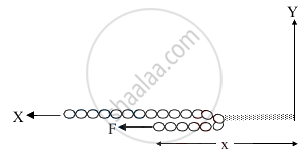
Let the point of application of force have moved by distance 'dx'.

∴ Work done by friction,

`W_f = int_0^{2L}-mu(M/L.x)g  dx`

⇒ `W_f = -Mgl`

`W_f = 2Fl`

∴ `W_{"net"} = 2FL - muMgL ⇒ 1/2Mv^2`

= 2FL - μMgL

 ⇒ `v = {2((2F)/M - mug)L}^{1/2}`