Question

A charged particle (mass m and charge q) moves along X axis with velocity V₀. When it passes through the origin it enters a region having uniform electric field `vec"E" = -"E"hat"j"` which extends upto x = d. Equation of path of electron in the region x > d is :

Options

• y = `"qEd"/("mV"_0^2)x`

• y = `"qEd"/("mV"_0^2)(x-"d")`

• y = `"qEd"/("mV"_0^2)("d"/2-x)`

• y = `"qEd"^2/("mV"_0^2)x`

Answer 1

`bb("y" = "qEd"/("mV"_0^2)("d"/2-x))`

Explanation:

Given: Mass of a particle is m, charge on particle is q, initial velocity of particle before entering the region of electric field is v₀ `vec"i"`, electric field `vec"E"= -"E"hat"j"` exists in the region x = 0 to x = d.

To find: The equation of the particle for the region x > d.

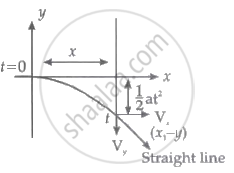
After passing through the electric field, the particle's velocity components will change as follows:

V_x = V_0, V_y = at, a =`-"qE"/"m"`.

In the region x > d, the equation of the particle will be a straight line.

`("y"-1/2"at"^2)/(x-"d") = "at"/"V"_0`

`("y"-1/2"at"^2)/"at" = (x-"d")/"V"_0`

`"y"/"at" - 1/2"d"/"V"_0 = x/"V"_0-"d"/"V"_0`

`"y"/"at" = x/"V"_0 - 1/2"d"/"V"_0`

`(-"ymV"_0)/"qEd" = x/"V"_0 - 1/2"d"/"V"_0`

y = `"qEd"/("mV"_0^2)("d"/2-x)`