Question

A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.

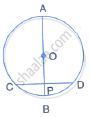
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB

 

Answer 1

OP⊥CD
∴ OP bisects CD
(Perpendicular drawn from the centre of a circle to a chord bisects it)

⇒ CP=`("CD")/2`

In right ΔOPC,

OC² =OP² + CP²

⇒ CP²= OC² - OP² =(15)² - (9)² = 144
∴ CP =12 cm
∴ CD =12×2 = 24 cm

(ii) Join BD
∴ BP = OB - OP = 15 - 9 = 6 cm
In right ΔBPD,
BD² = BP² + PD²

= (6)² + ( 12)² = 180

In ΔADB, ∠ADB = 90°

(Angle in a semicircle is a right angle)

∴  AB² = AD² + BD²

⇒  AD² = AB² + BD² = (30)² - 180 =720

∴ `"AD" =sqrt 720 = 26.83 "cm"`

(iii) Also, BC = BD `sqrt 180` =13.42 cm