Advertisements
Advertisements
Question
A cistern can be filled by a tap in 4 hours and emptied by an outlet pipe in 6 hours. How long will it take to fill the cistern if both the tap and the pipe are opened together?
Advertisements
Solution
\[\text{ Time taken by the tap to fill the cistern = 4 hours } \]
\[ \therefore \text{ Tap fills } \frac{1}{4}\text{ th part of the cistern in 1 hour } . \]
\[\text{ Time taken by the pipe to empty the cistern = 6 hours }\]
\[ \therefore \text{ Pipe empties out } \frac{1}{6}\text{ th part of the cistern in 1 hour } . \]
\[\text{ Thus, in 1 hour, } \left( \frac{1}{4} - \frac{1}{6} \right)\text { th part of the cistern is filled } . \]
\[\text{ We have: } \]
\[\frac{1}{4} - \frac{1}{6} = \frac{6 - 4}{24} = \frac{2}{24} = \frac{1}{12}\]
\[\text{ Thus, in 1 hour, } \frac{1}{12}\text{ th part of the cistern is filled .} \]
\[\text{ Hence, the cistern will be filled in 12 hours } .\]
APPEARS IN
RELATED QUESTIONS
Rohit bought 12 registers for Rs 156, find the cost of 7 such registers.
6 men can complete the electric fitting in a building in 7 days. How many days will it take if 21 men do the job?
Working 8 hours a day, Ashu can copy a book in 18 days. How many hours a day should he work so as to finish the work in 12 days?
A truck needs 54 litres of diesel for covering a distance of 297 km. The diesel required by the truck to cover a distance of 550 km is ______.
In a camp, there is enough flour for 300 persons for 42 days. How long will the flour last if 20 more persons join the camp?
From the following table, determine if x and y are in direct proportion or not.
| x | 1 | 4 | 9 | 20 |
| y | 1.5 | 6 | 13.5 | 30 |
Campus and Welfare Committee of school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In the following mixtures, decide which is a lighter shade of blue and also find the lightest blue shade among all of them.
| Mixture G | Mixture H |
 |
 |
If one container has one litre paint and the building requires 105 litres for painting, how many container of each type is required to paint the building by darkest blue shade?
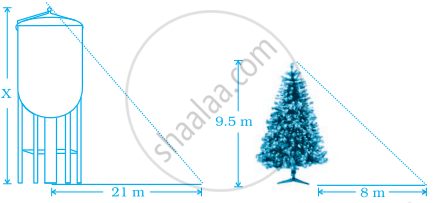
A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.
Here is a key board of a harmonium:
- Find the ratio of white keys to black keys on the keyboard.
- What is the ratio of black keys to all keys on the given keyboard.
- This pattern of keys is repeated on larger keyboard. How many black keys would you expect to find on a keyboard with 14 such patterns.
The students of Anju’s class sold posters to raise money. Anju wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise Rs 250 for every 60 posters sold.
- How much money would Anju’s class make for selling 102 posters?
- Could Anju’s class raise exactly Rs 2,000? If so, how many posters would they need to sell? If not, why?
