Advertisements
Advertisements
Question
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Solution
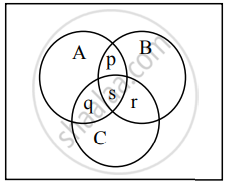
Let A = Set of students who received medals in volleyball.
B = Set of students who received medals in football.
C = Set of students who received medals in basketball.
n(A) = 38, n(B) = 15, n (C) = 20, n(A ∪ B ∪ C) = 58, n(A ∩ B ∩ C) = 3.
n(A ∪ B ∪ C)
= n(A) + n(B) + n(C) − n(A ∩ B) − n(B ∩ C) − n(A ∩ C) + n(A ∩ B ∩ C)
∴ 58 = 38 + 15 + 20 − n(A ∩ B) − n(B ∩ C) − n(A ∩ C) + 3
∴ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 .......(i)
Number of players who got exactly two medals = p + q + r
Here, s = n(A ∩ B ∩ C) = 3
n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 …[From (i)]
∴ p + s + s + r + q + s = 18
∴ p + q + r + 3s = 18
∴ p + q + r + 3(3) = 18
∴ p + q + r = 18 − 9 = 9
∴ Number of players who received exactly two medals = 9.
APPEARS IN
RELATED QUESTIONS
Identify whether the following is set or not? Justify your answer.
The collection of all months of a year beginning with the letter J.
Identify whether the following is set or not? Justify your answer.
The collection of ten most talented writers of India.
Identify whether the following is set or not? Justify your answer.
A collection of novels written by the writer Munshi Prem Chand.
Write the following set in the set-builder form:
{5, 25, 125, 625}
List all the elements of the following set:
D = {x : x is a letter in the word “LOYAL”}
Which of the following collection are sets? Justify your answer:
The collection of all question in this chapter.
Which of the following collection are sets? Justify your answer:
The collection of prime integers.
Describe the following sets in Roster form:
{x ∈ R : x > x}.
Describe the following sets in set-builder form:
B={1,1/2 ,1/3, 1/4,1/5,...........};
Describe the following sets in set-builder form:
C = {0, 3, 6, 9, 12, ...}
Which of the following statemen are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\phi \subset \left\{ a, b, c \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ c, d \right\} \subset A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ c, d \right\} \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ a, b, c \right\} \subset A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true?\[\left\{ \left\{ \phi \right\} \right\} \subset A\]
Write down all possible subsets of each of the following set:
{a, b, c},
Write down all possible proper subsets each of the following set:
{1}.
What is the total number of proper subsets of a set consisting of n elements?
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
4 _____ A
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
10 _____ A
Describe the following set in Set-Builder form
`{1/2, 2/5, 3/10, 4/17, 5/26, 6/37, 7/50}`
If A = {x/6x2 + x – 15 = 0}, B = {x/2x2 – 5x – 3 = 0}, C = {x/2x2 – x – 3 = 0} then find (A ∩ B ∩ C)
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read Only one of the newspapers
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to Chemical A or Chemical B
Write the following interval in Set-Builder form
`(6, ∞)`
Write the following interval in Set-Builder form
`(-∞, 5]`
Answer the following:
In a survey of 425 students in a school, it was found that 115 drink apple juice, 160 drink orange juice, and 80 drink both apple as well as orange juice. How many drinks neither apple juice nor orange juice?
Write the following sets in the roaster form.
A = {x | x is a positive integer less than 10 and 2x – 1 is an odd number}
Given that E = {2, 4, 6, 8, 10}. If n represents any member of E, then, write the following sets containing all numbers represented by n2
Let X = {1, 2, 3, 4, 5, 6}. If n represent any member of X, express the following as sets:
n + 5 = 8
State which of the following statements is true and which is false. Justify your answer.
496 ∉ {y | the sum of all the positive factors of y is 2y}.
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French and Sanskrit but not English
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French and English but not Sanskrit
The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
State True or False for the following statement.
Given A = {0, 1, 2}, B = {x ∈ R | 0 ≤ x ≤ 2}. Then A = B.
