Question

A cone of maximum volume is inscribed in a given sphere. Then the ratio of the height of the cone to the diameter of the sphere is ______.

Options

• `3/4`

• `1/3`

• `1/4`

• `2/3`

Answer 1

A cone of maximum volume is inscribed in a given sphere. Then the ratio of the height of the cone to the diameter of the sphere is `underlinebb(2/3)`.

Explanation:

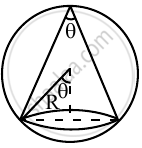
v = `1/3πR^2cos^2θ.R(1 + sinθ)`

`(dv)/(dθ) = R^3/3 (cos^3θ - 2cosθsinθ(1 + sinθ))` = 0

⇒ cos²θ = 2sinθ + 2sin²θ

(1 – sinθ)(1 + sinθ) = 2sinθ(1 + sinθ)

⇒ sinθ = `1/3`

h = `4/3`R

⇒ `h/(2R) = 2/3`