Question

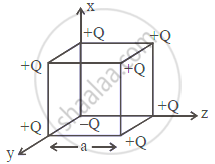
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is ______.

Options

• `(2"Q")/(3sqrt3piepsilon_0a^2) (hatx +hat"y" +hat"z")`

• `"Q"/(3sqrt3piepsilon_0a^2) (hatx +hat"y" +hat"z")`

• `(-2"Q")/(3sqrt3piepsilon_0a^2) (hatx +hat"y" +hat"z")`

• `(-"Q")/(3sqrt3piepsilon_0a^2) (hatx +hat"y" +hat"z")`

Answer 1

A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is `bb((-2"Q")/(3sqrt3piepsilon_0a^2) (hatx +hat"y" +hat"z"))`.

Explanation:

We can swap out the -Q charge at the problem's genesis for +Q and -2Q to simplify the issue.

The electric field created by the corners +Q charge at the cube's centre will now be zero.

As a result, the -2Q charge of the origin's net electric field in the centre will function.

`vec"E"= ("kq"  vec"r")/r^3 = (1(-2"Q")a/2(hatx+haty+hatz))/(4piepsilon_0(a/2sqrt3)^3)`

`vec"E" = (-2"Q"(hatx+haty+hatz))/(3sqrt3pia^2epsilon_0)`